Ôn tập: 20 câu ôn bài tập công suất dòng điện xoay chiều

Dưới đây là video bài giảng Ôn tập: 20 câu ôn bài tập công suất dòng điện xoay chiều tổng hợp một số câu trắc nghiệm về công suất mạch xoay chiều nhằm giúp các em học sinh 12 ôn tập lại bài và củng cố kiến thức đã học. 

Câu 1: Mạch điện chỉ có R với điện trở R = 100W một nguồn điện tổng hợp có biểu thức u =100 + 100cos(100\(\pi\)t + \(\pi\)/2) V. Tính công suất tỏa nhiệt trên điện trở:

      A. 50W                                B. 200W                          C. 25W                              D. 150W.

Lời giải
\(R=100\Omega , u=100-100\sqrt{2}cos(100\pi +\frac{\pi }{2})\)
\(\Rightarrow P=\frac{100^2}{100}+\frac{100^2}{100}=200W\)

Câu 2: Mạch điện xoay chiều RLC ghép nối tiếp, đặt vào hai đầu mạch một hiệu điện thế u = U₀cos\(\pi\)t (V). Điều chỉnh C = C₁ thì hệ số của mạch là cosφ₁ = \(\frac{1}{2}\)  và khi đó công suất của mạch là P = 50W. Điều chỉnh C = C₂ thì hệ số công suất của mạch là \(\frac{\sqrt{3}}{2}\). Công suất của mạch khi đó là:

      A. 200W                              B. 150 W                         C. 100W                            D. 300W

Lời giải
\(C=C_1\Rightarrow cos\varphi _1=\frac{1}{2}\Rightarrow P_1=50W\)\(C=C_2\Rightarrow cos\varphi _2=\frac{\sqrt{3}}{2}\Rightarrow P_2=?\)
\(P=\frac{U^2}{R}.cos^2\varphi \Rightarrow \frac{P_2}{P_1}=\frac{cos^2\varphi _2}{cos^2\varphi _1} =3\)
\(\Rightarrow P_2=3P_1=150W\)

Câu 3: Mạch điện xoay chiều RLC ghép nối tiếp, đặt vào hai đầu mạch một hiệu điện thế u = U₀cos\(\pi\)t (V). Điều chỉnh C = C₁ thì hệ số của mạch là cosφ₁ = \(\frac{1}{\sqrt{2}}\) và khi đó công suất của mạch là P = 50W. Điều chỉnh C = C₂ thì hệ số công suất của mạch là \(\frac{1}{2}\) . Công suất của mạch khi đó là:

      A. 25W                                B. 150 W                         C. 100W                            D. 50W

Lời giải
\(\frac{P_2}{P_1}=\frac{cos^2\varphi _2}{cos^2\varphi _1}=\frac{1}{4}*2=\frac{1}{2 }\Rightarrow P_2=\frac{P_1}{2}\)
\(\Rightarrow P_2=25W\)

Câu 4: Dòng điện xoay chiều có biểu thức: \(i=2cos100\pi t\) (A) qua mạch chỉ có điện trở R = 50 \(\Omega\). Nhiệt lượng tỏa ra trên R trong 1 phút là

A. 100 J                             B. 6000 J.                    C. 3600 J.                    D. 1200 J

Lời giải
\(i=2cos \ 100 \pi t (A), R=50\Omega , t=60s\)
\(Q=Pt=RI^2.t=50(\frac{2}{\sqrt{2}})^2*60=6000J\)

Câu 5: Đặt vào hai đầu đoạn mạch R , L , C mắc nối tiếp một điện áp \(u=200\sqrt{2}sin\omega t (V)\). Biết R = 100 \(\Omega\) và \(\omega\) thay đổi. Khi điện áp giữa hai bản tụ điện lệch pha \(\frac{\pi}{3}\) so với điện áp hai đầu mạch thì công suất tiêu thụ của mạch bằng

A. 100 W.                          B. \(200\sqrt{3}\) W                C. 300 W.                    D. 200 W .

Lời giải
u_C lệch pha \(\frac{\pi}{3}/u\Rightarrow \varphi =-\frac{\pi }{6}\)
\(\Rightarrow P=\frac{U^2}{R}.cos^2 \varphi =\frac{200^2}{100}*\frac{3}{4}=300W\)

Câu 6: Cho mạch điện AB gồm một biến trở R; một cuộn cảm có điện trở thuần bằng 60 \(\Omega\) và một tụ điện mắc nối tiếp. Đặt vào A, B một điện áp u = U₀cos\(\omega\)t luôn ổn định thì cảm kháng của cuộn cảm và dung kháng của tụ điện lần lượt là 172 \(\Omega\) và 92 \(\Omega\). Cho R thay đổi thì thấy công suất tiêu thụ trên biến trở có giá trị lớn nhất bằng 144 W. Giá trị của U₀ là

            A. \(48\sqrt{10}\)V.                 B. \(96\sqrt{10}\) V.                 C. \(96\sqrt{5}\)V.                  D. \(48\sqrt{5}\) V.

Lời giải

\(R\Rightarrow (P_R)_{max}=144W\Rightarrow R=\sqrt{r^2+Z_{LC}^2}=100\)
\(P_R_{max}=R*\frac{U^2}{(R+r)^2+Z^2_LC}=100*\frac{U^2}{160^2+80^2}=144\)\(\Rightarrow U=96\sqrt{5}V\Rightarrow U_0=U\sqrt{2}=96\sqrt{10}\)

Câu 7: Cho mạch điện AB gồm một gồm một bóng đèn dây tóc có ghi (120 V-75 W) và một cuộn cảm có độ tự cảm \(\frac{{3,2}}{\pi }H\) mắc nối tiếp. Đặt vào A, B một điện áp xoay chiều u có tần số 50 Hz thì thấy đèn hoạt động đúng công suất định mức và khi đó công suất tiêu thụ của mạch AB bằng 93,75 W. Điện áp hiệu dụng giữa hai đầu cuộn cảm xấp bằng

            A. 220 V.                     B. 200 V.                     C. 250 V.                     D. 202 V

Lời giải

R_Đ \(=\frac{U^2}{P}=\frac{120^2}{75}=192\Omega\)
\(Z_L=L.2\pi f=320\Omega\)
\(I=I_{dm}=\frac{P}{U}=\frac{75}{120}=\frac{5}{8}(A)\)
P = (R_Đ + r) I² ⇒ 93,75=(192+r). \(\frac{25}{64}\)
\(\Rightarrow r=48\Omega\)
\(U_d=I.Z_d=I.\sqrt{r^2+Z_L^2}=\frac{5}{8}*\sqrt{48^2+320^2}\approx 202V\)

Câu 8: Đoạn mạch AB gồm một tụ điện C mắc nối tiếp với một biến trở có giá trị từ 0 đến 600 \(\Omega\). Điện áp giữa hai đầu đoạn mạch u_AB = U\(\sqrt{2}\) cos\(\omega\)t. Điều chỉnh con chạy để biến trở có giá trị R = 400 \(\Omega\) thì công suất tỏa nhiệt trên biến trở max và bằng 100 W. Khi công suất toả nhiệt trên biến trở là 80 W thì biến trở có giá trị

            A. 200  \(\Omega\)                    B. 300 \(\Omega\)                      C. 400 \(\Omega\)                      D. 500 \(\Omega\)

Lời giải
\(RC: \ R\in [0;600\Omega ]\)
\(R_0=400\Rightarrow \left\{\begin{matrix} P_{max}=100=\frac{U^2}{2*400}\\ Z_C=R_0=400 \end{matrix}\right.\)\(P=80W=R*\frac{U^2}{R^2+Z^2_C}\)
\(\Rightarrow 80=R*\frac{2*400*100}{R^2+400^2}\)
\(\Rightarrow R^2-1000R+400^2=0\)
\(\Rightarrow \bigg \lbrack\begin{matrix} R=200\Omega \ \ \ \ \ \ \ \ \ \ \\ R=800\Omega \ \ (loai) \end{matrix}\)

Câu 9: Cho đoạn mạch điện không phân nhánh AB gồm một điện trở bằng 10 \(\Omega\), một cuộn cảm thuần có độ tự cảm \(\frac{1}{10 \pi}\) H và một tụ điện có điện dung C. Điện áp tức thời giữa hai bản tụ điện là u = 100cos100\(\pi\)t (V). Công suất tiêu thụ của mạch AB bằng 250 W. Điện dung C có giá trị

A. \(\frac{10^-^3}{\pi} F\).                  B. \(\frac{10^-^3}{2\pi} F\).                   C. \(\frac{10^-^3}{4\pi} F\).                   D. \(\frac{10^-^3}{8\pi} F\).

Lời giải
\(R=10;Z_L=L.\omega =10.U=50\sqrt{2}\)
\(P=250W\Rightarrow R^2-\frac{U^2}{P}*R+(Z_L-Z_C)^2=0\)
\(\Rightarrow \left | 10-Z_C \right |=\sqrt{\frac{2.50^2}{250}*10-10^2} =10\)

\(\Rightarrow Z_C=20\Rightarrow C=\frac{10^-^3}{2\pi}F\)

Câu 10: Một đoạn mạch xoay chiều gồm một điện trở thuần R = 100 \(\Omega\), cuộn cảm thuần có độ tự cảm L và một tụ điện có điện dung \(C=\frac{10^{-4}}{\pi}F\) mắc nối tiếp giữa hai điểm có hiệu điện thế u = 200\(\sqrt{2}\)cos100\(\pi\)t (V). Công suất của mạch khi đó 200 W

A. \(\frac{1}{2\pi}H\) .                     B. \(\frac{4}{\pi}H\) .                       C. \(\frac{2}{\pi}H\) .                       D. \(\frac{1}{\pi}H\) .

Lời giải
\(R=100;Z_C=\frac{1}{\omega }=100;U=200\)
\(P=200W\Rightarrow R^2-\frac{U^2}{P}.R+(Z_L-Z_0)^2=0\)
\(\Rightarrow \left | Z_L-100 \right |=\sqrt{\frac{200^2}{200}*100-100^2}=100\)

\(\Rightarrow Z_L=200\Rightarrow L=\frac{2}{\pi}(H)\)

Câu 11: Cho mạch gồm cuộn dây (R₀ = 20\(\Omega\); L) mắc nối tiếp với tụ C có điện dung thay đổi và điện trở R. Điện áp hai đầu mạch u = 100\(\sqrt{2}\) cos100pt (V).  Khi thay đổi C đến giá trị C₀ thì công suất mạch cực đại và bằng 200 W, giá trị R là

            A. 10\(\Omega\)                    B. 20\(\Omega\)         C. 30\(\Omega\)                                D. 40\(\Omega\)

Lời giải

\(u=100\sqrt{2}cos100 \pi t (V)\)
\(c=c_0\Rightarrow P_{max}=200W=\frac{U^2}{R_0+R}\)
\(R_0+R=\frac{U^2}{200}=\frac{100^2}{200}=50\Rightarrow R=30\Omega\)

Câu 12: Đặt một điện áp xoay chiều u = 100 \(\sqrt{2}\)cos(100\(\pi\)t + \(\frac{\pi }{3}\)) (V) vào hai đầu đoạn mạch mắc nối tiếp gồm biến trở, tụ điện và cuộn dây có điện trở hoạt động là r = 30 \(\Omega\). Biết cảm kháng và dung kháng của mạch lần lượt là 100\(\Omega\) và 60\(\Omega\). Thay đổi giá trị của biến trở thì công suất tiêu thụ của cuộn dây đạt cực đại bằng

            A. 40 W                       B. 31,25 W                  C. 120 W                     D. 50 W

Lời giải

\(u=100\sqrt{2}cos(100\pi +\frac{\pi }{3});r=30\)
\(\left\{\begin{matrix} Z_L=100\\ Z_C=60 \ \ \end{matrix}\right.\)
\(P_r=r.\frac{U^2}{(R+r)^2+Z^2_u}\Rightarrow \left\{\begin{matrix} (P_r)_{max}=\frac{r*U^2}{r^2+Z_u^2}=120W\\ R=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix}\right.\)

Câu 13: Cho đoạn mạch điện không phân nhánh gồm một cuộn cảm và một tụ điện có điện dung \(\frac{1,25}{9\pi}.10^{-3}F\). Giữa hai đầu đoạn mạch có một điện áp u = 120cos2 \(\pi\)ft (V) với tần số f thay đổi được. Cho f thay đổi. Khi f =  50Hz thì hiệu điện thế giữa hai đầu cuộn cảm lệch pha 45⁰ so với cường độ dòng điện. Khi f = 60Hz thì công suất tiêu thụ của mạch có giá trị lớn nhất là P_Max. Giá trị của P_Max bằng

            A.  240 W.                   B.  120 W.                   C.  144 W.                   D.  288 W.

Lời giải
\(f=50Hz\Rightarrow \varphi _d=45^0\Rightarrow R=Z_L\)
\(f=60Hz\Rightarrow \left\{\begin{matrix} P_{max}=\frac{U^2}{R}=?\\ Z_L2=Z_C2=\frac{1}{C.2\pi f} \end{matrix}\right.\)
\(\Rightarrow Z_{L2}=\frac{1}{\frac{1,25}{9\pi}*10^-^3*2\pi *60}= \frac{900}{1,25*2*6}=60\)
\(\Rightarrow \frac{Z_{L2}}{Z_{L1}}=\frac{L_2\pi f_2}{L_2\pi f_1}= \frac{f_2}{f_1}=\frac{6}{5}\Rightarrow Z_L_1=50\)
\(\Rightarrow R=50\Omega\)
\(P_{max}=\frac{(\frac{120}{\sqrt{2}})^2}{50}=\frac{2.60^2}{50}=144W\)

Câu 14: Mạch điện gồm một biến trở R mắc nối tiếp với cuộn dây thuần cảm . Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều ổn định \(u=U_0cos100\pi t(V)\). Thay đổi R ta thấy với hai giá trị \(R_1=45\Omega\) và \(R_2=80\Omega\) thì mạch tiêu thụ công suất đều bằng 80W. Giá trị cực đại của công suất tiêu thụ trên mạch khi thay đổi R là

            A. 250 W.                    B. \(\frac{250}{3}\).                    C. \(80\sqrt{2}\) W.                 D.100 W.

Lời giải
\(\left\{\begin{matrix} R_1=45\Omega \\ R_2=50\Omega \end{matrix}\right.\Rightarrow P_1=P_2=80W\)
R thay đổi \(\Rightarrow P_{max}=\frac{U^2}{2R_0}\)
\(R_0=\sqrt{R_1R_2}=\sqrt{45.80}=60\Omega\)
\(R_1+R_2=\frac{U^2}{P}\Rightarrow U^2=P(R_1+R_2)\)
\(\Rightarrow U^2=80(45+80)=80*125\)
\(\Rightarrow P _{max}=\frac{80.125}{2.60}=\frac{250}{3}W\)

Câu 15: Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch RLC không phân nhánh. Tần số của mạch có giá trị thay đổi được. Khi f = f₁ = 50 Hz thì hệ số công suất của mạch đạt cực đại. Khi f = f₂ = 100 Hz thì hệ số công suất của mạch bằng 0,5. Khi f = f₃ = 150 Hz, hệ số công suất của mạch xấp xỉ bằng

            A. 0,3                          B. 0,25                         C. 0,4                           D.  0,21

Lời giải
\(f=f_1=50\Rightarrow cos\varphi _1=1\Rightarrow Z_L_1=Z_C_1 \ \ (1)\)
\(f=f_2=100\Rightarrow cos\varphi _2=0,5 \ \ (2)\)
\(f=f_3=150\Rightarrow cos\varphi _3=\frac{R}{R^2+(Z_L_3-Z_C_3)} \ \ (3)\)

Từ (2) \(\Rightarrow \frac{R}{\sqrt{R^2+(Z_L_2-Z_C_2)^2}}=0,5 \Rightarrow \left | Z_L_2-Z_C_2 \right |=R\sqrt{3}\)
Mà \(f_2=2f_1\Rightarrow \left\{\begin{matrix} Z_L_1=2Z_L_1\\ Z_C_2=\frac{Z_C_1}{2}=\frac{Z_L_1}{2} \end{matrix}\right.\)
\(\Rightarrow \left | 2Z_L_1-\frac{Z_L_1}{2} \right |=R\sqrt{3} \Rightarrow \frac{3Z_L_1}{2}=R\sqrt{3}\Rightarrow Z_L_1=\frac{2R}{\sqrt{3}}\)
Mà \(f_3=3f_1\Rightarrow \left\{\begin{matrix} Z_L_3=3Z_L_1=2\sqrt{3}R\\ Z_C_3=\frac{Z_C_1}{3}=\frac{2R}{3\sqrt{3}} \end{matrix}\right. \ \ (4)\)

Từ (2) (3) \(cos \varphi _3=0,3\)

Câu 16: Mạch RLC nối tiếp, cuộn dây thuần cảm. Mắc vào 2 đầu mạch điện áp xoay chiều u = U₀cos(2\(\pi\)ft)với f thay đổi được. Khi f = f₁ = 36Hz và f = f₂ = 64Hz thì công suất tiêu thụ của mạch là như nhau P₁ = P₂. Khi f = f₃ = 48Hz thì công suất tiêu thụ của mạch là P₃, khi f = f₄ = 50Hz thì công suất tiêu thụ của mạch là P₄. So sánh các công suất ta có

            A. P₄ < P₃.                    B. P₄ < P₂.                    C. P₃ < P₁.                    D. P₄ > P₃.

Lời giải
\(\left\{\begin{matrix} f=f_1=36Hz\\ f=f_2=64 \end{matrix}\right.\Rightarrow P_1=P_2\)
\(f=f_3=48\Rightarrow P_3\)
\(f=f_4=50\Rightarrow P_4\)
\(P_{max}\Rightarrow f_0=\sqrt{f_1.f_2}=\sqrt{36.64}=48Hz\)
\(\Rightarrow f_3=f_0\Rightarrow P_3=P_{max}>P_4\)
*
\(\left | f_4-f_0 \right |=2\)
\(\left | f_2-f_0 \right |=16\)
\(\Rightarrow \left | f_4-f_0 \right |< \left | f_2-f_0 \right |\Rightarrow P_4>P_2\)

Câu 17: Đặt điện áp \(u=U_0cos\omega t\) vào hai đầu đoạn mạch gồm cuộn cảm thuần, tụ điện, biến trở R thứ tự mắc nối tiếp với nhau. Ứng với hai giá trị R₁ và R₂ = 4R₁ của biến trở thì công suất tiêu thụ trong đoạn mạch đều bằng 390 W. Khi giá trị của biến trở là R = 3R₁ thì công suất tiêu thụ của mạch là

            A. 292,5 W                  B. 450 W                     C. 130 W                     D. 487,5 W

Lời giải
\(\left\{\begin{matrix} R_1\\ R_2=4R_1 \end{matrix}\right.\Rightarrow P_2=P_1=390W\)
\(R=3R_1\Rightarrow P=R\frac{U^2}{R^2+Z^2_{LC}}= 3R_1.\frac{U^2}{9R_1^2+Z_{LC}^2}\)
\(R_0^2=Z^2_LC=R_1R_2=4R^2_1\)
\(R_1+R_2=\frac{U^2}{P_1}\Rightarrow 5R_1=\frac{U^2}{390}\)
\(P=3R_1.\frac{5R_1.390}{9R^2_1+4R^2_1}= \frac{3.5.390}{13}=450W\)

Câu 18: Cho mạch điện gồm RLC mắc nối tiếp, L thay đổi được, tụ điện có điện dung  \(C=\frac{10^{-3}}{4\pi}\)F. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định có tần số 50 Hz. Khi L = L₀ thì điện áp hai đầu tụ vuông pha với điện áp hai đầu mạch và công suất tiêu thụ của mạch lúc này bằng P₀. Khi \(L=L_1=\frac{9}{10\pi}\) H thì công suất tiêu thụ mạch là P₁. Khi \(L=L_2=\frac{7}{5\pi}\) H thì công suất tiêu thụ mạch là P₂. Chọn phát biểu đúng.

            A. P₀ > P₁ > P₂.             B. P₀ > P₂ > P₁.             C. P₀ < P₁ < P₂.             D. P₀ < P₂ < P₁.

Lời giải
\(L=L_0\Rightarrow \left\{\begin{matrix} u_c\perp u\Rightarrow CHD=f_0=50\\ P_0=P_{max} \end{matrix}\right.\)
\((\Rightarrow L_0=\frac{1}{4\pi^2f^2.c})=\frac{1}{4\pi^2.50^2 .\frac{10^{-3}}{4\pi }}=\frac{2}{5\pi}Hz\)
\(f_1=\frac{1}{2\pi\sqrt{L_2C}}=\frac{1}{2\pi\sqrt{\frac{9}{10\pi}*\frac{10^{-3}} {4\pi}}}=33,3Hz\)
\(f_2=\frac{1}{2\pi\sqrt{L_2C}}=\frac{1}{2\pi\sqrt{\frac{7}{5\pi}*\frac{10^{-3}}{4\pi }}}=26,7Hz\)
\(\Rightarrow \left\{\begin{matrix} \left | f_1-f_0 \right |=16,7\\ \left | f_2-f_0 \right |=23,3 \end{matrix}\right.\Rightarrow \left | f_1-f_0 \right | <\left | f_2-f_0 \right |\)
\(\Rightarrow P_1>P_2\)
\(\Rightarrow P_0>P_1>P_2\)

Câu 19: Một đoạn mạch điện xoay chiều gồm: Một điện trở thuần R, một cuộn cảm thuần có độ tự cảm L = \(\frac{1}{\pi}H\) và tụ điện có điện dung C thay đổi được mắc nối tiếp với nhau. Điện áp đặt vào hai đầu mạch có biểu thức \(u=220\sqrt{2}cos(100 \pi t +\frac{\pi}{3})\)(V). Khi cho C thay đổi thì thấy khi C = C₁ và khi C = C₂  mạch tiêu thụ cùng một công suất và dung kháng của tụ khi C = C₁ gấp 9 lần khi C = C₂. C₁ và C₂ nhận giá trị nào sau đây?

            A. \(C_1=\frac{10^{-4}}{3\pi}F;C_2=\frac{10^{-4}}{27\pi}F\)                              

           B. \(C_1=\frac{10^{-3}}{\pi}F;C_2=\frac{10^{-3}}{9\pi}F\)

            C. \(C_1=\frac{10^{-4}}{2\pi}F;C_2=\frac{10^{-3}}{18\pi}F\)                               

            D. \(C_1=\frac{10^{-3}}{18\pi}F;C_2=\frac{10^{-4}}{2\pi}F\)

Lời giải
\(\left\{\begin{matrix} C_1\\ C_2\\ Z_{C_1}=9Z_C_2 \end{matrix}\right.\Rightarrow P_1=P_2\)
\(\Rightarrow Z_C_1+Z_C_2=2Z_L=2.L.\omega =200\)
\(\Rightarrow \left\{\begin{matrix} Z_C_1=9Z_C_2\\ Z_C_1+Z_C_2=200 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} Z_C_1=180\Omega \\ Z_C_2=20\Omega \end{matrix}\right.\)

\(C_1=\frac{1}{Z_C_1.\omega }=\frac{1}{180.100\pi}=\frac{10^{-3}}{18\pi}F\)
\(C_2=\frac{1}{Z_C_2.\omega }=\frac{1}{20.100\pi}=\frac{10^{-3}}{2\pi}F\)
 

Câu 20: Hình bên là đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ P của đoạn mạch điện RLC không phân nhánh theo điện dung C của tụ điện. Biết điện áp giữa hai đầu đoạn mạch là \(u=220\sqrt{2}sin120\pi t\)(V) luôn ổn định. C₀ có giá trị bằng

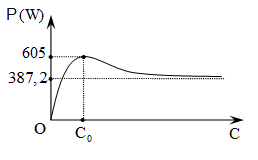
              A. \(\frac{10^{-2}}{12\pi}F\) .                 B. \(\frac{10^{-3}}{36\pi}F\) .

              C. \(\frac{10^{-2}}{72\pi}F\) .                 D. \(\frac{10^{-3}}{6\pi}F\) . 

Lời giải
\(P_{max}=\frac{U^2}{R}=605\Rightarrow R=\frac{220^2}{605}=80\Omega\)
\(Z_C=0\Rightarrow P=R.\frac{U^2}{R^2+Z_L^2}=387,2\)
\(\Rightarrow 80.\frac{220^2}{80^2+Z^2_L}=387,2\Rightarrow Z_L=60\Omega\)
\(\Rightarrow Z_C_0=Z_L=60\Rightarrow C_0= \frac{1}{60.120\pi}=\frac{10^{-2}}{72 \pi}F\)