Bài 1: Dao động điều hòa

Bài học giúp các em nắm được những kiến thức cơ bản về:

1. Các phương trình dao động điều hòa:

• Phương trình li độ.
• Phương trình vận tốc.
• Phương trình gia tốc.

2. Mối liên hệ về pha - Công thức độc lập với thời gian

• Mối liên hệ về pha.
• Công thức độc lập thời gian.

3. Liên hệ giữa chuyển động tròn đều và dao động điều hòa.

Năm lớp 10 của chương trình Vật lý cấp 3 em đã học được khái niệm chuyển động gồm: chuyển động đều, chuyển động biến đổi đều, chuyển động rơi tự do. Khái niệm chuyển động là sự thay đổi vị trí của vật so với vật khác theo thời gian, có nghĩa là em phải chọn vật làm mốc. Như vậy, ở chương trình Vật lý 12, dao động có phải là chuyển động hay không?

 Ví dụ: một chiếc lá khi không có gió thì đứng yên, khi có gió chiếc lá sẽ đu đưa qua lại, không có gió lại dừng, đó chính là dao động. Vị trí không có gió là vị trí cân bằng, còn có gió sẽ đu đưa qua lại quanh vị trí cân bằng. Dao động là chuyển động được lập đi lập lại quanh vị trí cân bằng có giới hạn. Trong vô số dao động, dao động đơn giản nhất là dao động điều hoà. Vậy dao động điều hoà là gì?

1. Các phương trình dao động điều hòa

a. Phương trình li độ

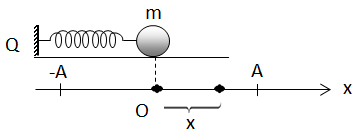
+ Định nghĩa: Dao động điều hòa là dao động được mô tả theo quy luật sin hoặc cosin của thời gian.
\(x = A.cos(\omega t + \varphi )\)
Với:
x: li độ (tọa độ)
A: biên độ (li độ cực đại)
\(\omega\): tần số góc 
\(\omega t + \varphi\): pha dao động
\(\varphi\): pha ban đầu (Tại t = 0)
b. Phương trình vận tốc
\(v = \frac{\Delta x}{\Delta t} = x'(t)\)
\(v = - \omega A.sin(\omega t+\varphi ) = \omega Acos(\omega t + \varphi + \frac{ \pi}{2})\)
\(\rightarrow v = v_{max}.cos(\omega t + \varphi + \frac{ \pi}{2}),v_{max} = \omega A\)

• \(v_{max} = \omega A\): vận tốc cực đại (VTCB, v > 0)
• \(v_{min} = -\omega A\): vận tốc cực tiểu (VTCB, v < 0)
• \(|v|_{max} = \omega A\): tốc độ cực đại (VTCB)
• \(|v|_{min} = 0\): tốc độ cực tiểu (VT biên)

c. Phương trình gia tốc
\(a = \frac{\Delta v}{\Delta t} = v'(t)\)
\(\rightarrow a = x''(t)\)
\(\rightarrow a = -\omega ^2 \underbrace{ A.cos(\omega t + \varphi ) }_{x} \Rightarrow a = - \omega ^2.x\)

• \(\left | a \right | _{max} = \omega ^2.A\): vật ở 2 biên
• \(\left | a \right | _{min} = 0\): vật ở VTCB

2. Mối liên hệ về pha – Công thức độc lập với thời gian
a. Mối liên hệ về pha
Ta có: \(\left \{\begin{matrix} x = A.cos(\omega t + \varphi ) \hspace{2,5cm}\\ v = v_{max} .cos(\omega t + \varphi + \frac{\pi}{2}) \hspace{1,2cm}\\ a = - \omega ^2.x = - \omega ^2.A.cos(\omega t + \varphi ) \end{matrix}\right.\)

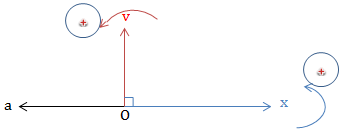
+ v nhanh pha \(\frac{\pi}{2}\) so với x (vuông pha)
+ a nhanh pha \(\frac{\pi}{2}\) so với v (vuông pha)
+ a ngược pha x
b. Công thức độc lập với thời gian
Ta có: \(\left \{\begin{matrix} x = A.cos(\omega t + \varphi ) \ \ \ \ \ \\ v = -v_{max} .sin(\omega t + \varphi )\\ a = - a_{max}.cos(\omega t + \varphi ) \end{matrix}\right.\)
NHỚ: \(sin^2(\omega t + \varphi ) + cos^2(\omega t + \varphi ) = 1\)
\(\cdot \ x\perp v : \left\{\begin{matrix} \frac{x}{A}=cos(\omega t + \varphi )\\ \frac{v}{v_{max}}=-sin(\omega t + \varphi ) \end{matrix}\right.\)
\(\left ( \frac{x}{A} \right )^2 + \left ( \frac{v}{v_{max}} \right )^2 = 1 \Rightarrow A^2 = x^2 + \left ( \frac{v}{\omega } \right )^2\)
\(\cdot \ a\perp v : \left\{\begin{matrix} \frac{a}{a_{max}}=-cos(\omega t + \varphi )\\ \frac{v}{v_{max}}=-sin(\omega t + \varphi ) \end{matrix}\right.\)
\(\Rightarrow \left ( \frac{a}{a_{max}} \right )^2 + \left ( \frac{v}{v_{max}} \right )^2 = 1\)
\(\Rightarrow A^2 = \left ( \frac{a}{\omega ^2} \right )^2 + \left ( \frac{v}{\omega ^2} \right )^2 = 1 \ \ \ (a = -\omega ^2x)\)

3. Liên hệ giữa chuyển động tròn đều và dao động điều hòa
Xét 1 vật có khối lượng m, chuyển động tròn đều với tốc độ góc ⍵ trên đường tròn tâm O, bán kính R = A

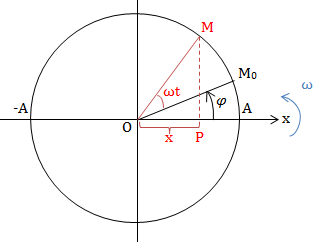
Ta có: \(x = \overline{OP} = A.cos(\omega t + \varphi )\)
Vậy: hình chiếu của 1 chuyển động tròn đều lên 1 trục nằm trong mặt phẳng quỹ đạo là 1 DĐĐH.
* Các đại lượng tương ứng giữa chuyển động tròn đều và DĐĐH.

* Ta có:
\(\\ 2 \pi\rightarrow T\\ \alpha \ \rightarrow \Delta t = \frac{\alpha .T}{2 \pi}\)

4. Lực hồi phục: là lực làm vật dao động điều hòa, luôn hướng về VTCB nên còn gọi là lực kéo về.
Biểu thức: \(F_{hp} = ma = -m\omega ^2x\)

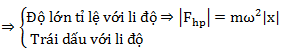
⇒ F_hp cùng pha với gia tốc.
\(| F_{hp}|_{max} = m\omega ^2A; | F_{hp}|_{min} = 0\) (Lưu ý: m đổi ra kg, A đổi ra m)