Dạng 8: Tìm thời gian ∆t để vật đi được quãng đường S

Sau khi học bài học này, học sinh dễ dàng giải các bài toán xác định thời gian ∆t để vật đi được quãng đường S.

Ở dạng 7, chúng ta đã giải quyết các bài toán Tìm quãng đường S vật đi được trong thời gian ∆t. Và hôm nay chúng ta tìm hiểu dạng ngược lại là dạng 8 Tìm thời gian ∆t để vật đi được quãng đường S nào đó.

NHỚ:
\(\\ \cdot \ S = 4A \Rightarrow \Delta t = 1T\\ \cdot \ S = 2A \Rightarrow \Delta t = \frac{1}{2}T\)
* Xét \(\frac{S}{4A} = a\)
\(\\ \cdot \bigg \lbrack \begin{matrix} a = k \ \ \ \ \ \\ a = k + \frac{1}{2} \end{matrix} \ \ (k \in Z) \Rightarrow \Delta t = a.T \\ \\ \cdot \bigg \lbrack \begin{matrix} a \neq k \ \ \ \ \ \\ a \neq k + \frac{1}{2} \end{matrix} \ \ (k \in Z) \Rightarrow a = k + \frac{p}{q}\ (p < q) \\ \Rightarrow S = a.4A = (k + \frac{p}{q}).4A \\ \Rightarrow S = \underbrace{k.4A}_{\substack{k.T}} + \frac{p}{q}.4A = \underbrace{k.4A}_{\substack{k.T}} + \underbrace{S_0}_{\substack{\Delta t_0}}\)
* Xác định ∆t₀:
+ Xác định trạng thái t₁
+ Vẽ sơ đồ ⇒ Vẽ S₀ ⇒ ∆t₀
Vậy ∆t = k.T + ∆t₀

VD1: Cho dao động \(x = 5cos(4\pi t + \pi)\) (cm).
a. Tìm thời gian để vật đi được các quãng đường S₁ = 0,6 m, S₂ = 1,1 m; S₃ = 175 cm kể từ t = 0?
b. Tìm thời gian để vật đi được quãng đường 255 cm kể từ t = \(\frac{1}{6}\)s?
Giải:
\(4A = 4.5 = 20\ cm; T = \frac{2 \pi}{\omega } = 0,5s\)
a.
\(\\ \cdot \ \frac{S_1}{4A} = \frac{60}{20} = 3 \Rightarrow \Delta t = 3T = 1,5s \\ \cdot \ \frac{S_2}{4A} = \frac{110}{20} = 5,5 \Rightarrow \Delta t = 5,5T = 2,75s \\ \cdot \ \frac{S_3}{4A} = \frac{175}{20} = 8 + \frac{3}{4} \Rightarrow S_3 = \underbrace{8.4A}_{\substack{8T}} + \frac{3}{4}.4A = \underbrace{8.4A}_{\substack{8T}} + 15\)
t = 0 ⇒ x = -5 (cm); v = 0

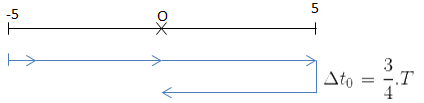
\(\Rightarrow \Delta t = 8.T + \frac{3}{4}.T = \frac{35}{4}.T = \frac{35}{8}(s)\)
b.
\(\frac{S}{4A} = \frac{255}{20} = 12 + \frac{3}{4} \Rightarrow S = \underbrace{12.4A}_{\substack{12.T}} + \frac{3}{4}.4A = \underbrace{12.4A}_{\substack{12.T}} +15\)
\(t = \frac{1}{6}s \Rightarrow x = 2,5\ cm;\ v > 0\)

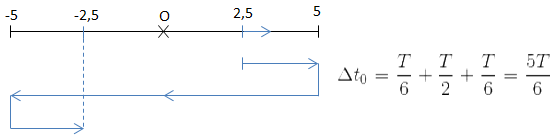
\(\Rightarrow \Delta t = 12T + \frac{5T}{6} = \frac{77T}{6}\)
\(\Rightarrow \Delta t = \frac{77}{12}s\)

VD2: Cho dao động \(x = 8cos(6\pi t - \frac{\pi}{3})\) (cm). Tìm thời gian để vật đi được quãng đường 1,75m kể từ t = 0?
Giải:
\(4A = 32 \ cm; \ T = \frac{2\pi}{\omega } = \frac{1}{3}s\)
Xét \(\frac{S}{4A} = \frac{175}{32} = 5 + \frac{15}{32}\)
\(S = \underbrace{ 5.4A }_{5T} + \frac{15}{32}.4A = \underbrace{ 5.4A }_{5T} + \underbrace{15}_{\Delta t_0}\)
Tại t = 0 ⇒ x = 4 cm; v > 0

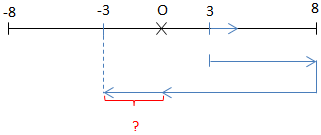
Xét: \(\Delta t = \frac{\alpha T}{2 \pi}\)
• Từ \(x = 0 \Rightarrow |x_0| < A \Rightarrow \alpha = arcsin \left ( \frac{|x_0|}{A} \right )\)
\(\Rightarrow \Delta t = \frac{T}{2 \pi} .arcsin \left ( \frac{|x_0|}{A} \right )\)
• Từ \(|x | = A \Rightarrow |x_0| \neq 0 \Rightarrow \alpha = arccos \left ( \frac{|x_0|}{A} \right )\)

\(\Rightarrow \Delta t = \frac{T}{2 \pi} .arccos \left ( \frac{|x_0|}{A} \right )\)
\(\\ \Rightarrow \Delta t_0 = \frac{T}{6} + \frac{T}{4} + \frac{T}{2 \pi} . sin^{-1}\left ( \frac{3}{8} \right ) \\ \Rightarrow \Delta t_0 = \left [ 5 + \frac{1}{6} + \frac{1}{4} + \frac{1}{2\pi} . sin^{-1}\left ( \frac{3}{8} \right ) \right ] . T \\ \Rightarrow \Delta t_0 = \left [ 5 + \frac{1}{6} + \frac{1}{4} + \frac{1}{2\pi} . sin^{-1}\left ( \frac{3}{8} \right ) \right ] . \frac{1}{3} \\ \Rightarrow \Delta t_0 \approx 1,826s\)