Dạng 2: Dao động tắt dần

Dao dộng tắt dần là một dạng khó và có sử dụng đến kiến thức lớp 10. Sau khi học bài này, các em sẽ nắm rõ được lý thuyết, hiểu rõ bản chất, hiểu phương pháp, nắm được cách làm bài liên quan đến dao động tắt dần. Qua đó biết được vị trí vật đạt tốc độ cực đại, tốc độ cực đại của vật, độ giảm biên độ sau một chu kỳ, số dao động và thời gian vật thực hiện dao động.

Hôm nay chúng ta tìm hiểu dạng 2: Dao động tắt dần, dạng này là dạng khó vì có sử dụng kiến thức của năm lớp 10. Vậy thế nào là dao động tắt dần? Dao động tắt dần là dao động có biên độ hoặc năng lượng giảm dàn theo thời gian do tác dụng của lực ma sát (đó là dao động thực tế).

Với bài toán dao động tắt dần, chúng ta chỉ xét dao động tắt dần chậm và dừng lại ở vị trí không biến dạng của lò xo. Nếu dao động tắt dần nhanh, đôi khi chưa thực hiện dao động đã dừng lại, không dừng lại ở VTCB là không dừng lại ở vị trí lò xo biến dạng ban đầu ⇒ Bài toán chỉ mang tính chất tương đối. Nếu như gặp bài toán này, chúng ta sẽ giải quyết theo cách khác và nó là bài toán tổng quát, khi chúng ta giải sẽ ra những kết quả đẹp nhất của dạng này và đề thi thường cho những kết quả nằm trong dạng này.

Xét 1 con lắc lò xo gồm một lò xo nhẹ có độ cứng k, vật nặng có khối lượng m đặt trên mặt phẳng ngang, hệ số ma sát giữa vật và sàn là \(\mu\). Từ VTCB đưa vật về vị trí lò xo bị biến dạng một đoạn X rồi buông cho vật dao động. Lấy gia tốc tại nơi đang xét là g.

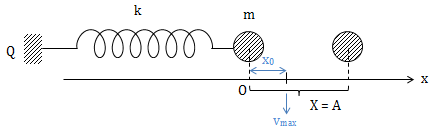
* Vị trí vật đạt tốc độ cực đại
Ta có:
\(F_{dh} = F_{ms} \Rightarrow k.x_0 = \mu N = \mu mg\)
\(\Rightarrow x_0 = \frac{\mu mg}{k}\)

* Tốc độ cực đại của vật
Ta có:
\(\frac{1}{2}kA^2 = \frac{1}{2}kx_0 ^2 + \frac{1}{2}mv^2 + \mu mg(A - x_0)\)
(Chọn gốc thế năng tại O)
\(\Rightarrow \frac{1}{2}mv^2 = \frac{1}{2}kA^2 - \frac{1}{2}kx_0 ^2 - \mu mg(A - x_0)\)
\(\Rightarrow \frac{1}{2}mv^2 = \frac{1}{2}kA^2 - \frac{1}{2}kx_0 ^2 - kx_0(A - x_0)\)
\(\Rightarrow mv^2 = kA^2 - kx_0 ^2 - 2kx_0(A - x_0)\)
                \(= k(A^2 - x_0 ^2 - 2x_0A - 2x_0 ^2)\)
                \(= k(A - x_0)^2\)
\(\Rightarrow v_{max} = \sqrt{(A - x_0)^2 . \frac{k}{m}} = \omega (A - x_0)\)

* Độ giảm biên độ sau một chu kỳ
Ta có:

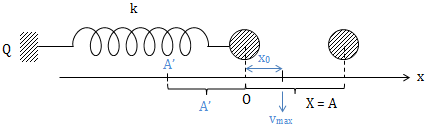
      \(\frac{1}{2}kA^2 = \frac{1}{2}k A'^{2} + \mu mg(A + A')\)
\(\Rightarrow \frac{1}{2}k(A^2 - A'^{2}) = \mu mg(A + A')\)
\(\Rightarrow \frac{1}{2}k(A- A')(A + A') = \mu mg(A + A')\)
\(\Rightarrow \Delta A' = A - A' = 2.\frac{\mu mg}{k} = 2x_0\)
Với \(\Delta A'\): độ giảm biên độ sau \(\frac{1}{2}T\)

* Số dao động vật thực hiện được đến khi dừng
\(N = \frac{A}{\Delta A} = \frac{A}{4x_0}\)

* Thời gian vật thực hiện dao động đến khi dừng
\(\Delta t = N.T = \frac{A}{x_0}. 2 \pi \sqrt{\frac{m}{k}}\)

* Đối với con lắc đơn
\(F_c = F_{ms}; \ m\omega ^2 = k\)

VD1: Một con lắc lò xo gồm 1 lò xo có độ cứng k = 1 N/m, vật nặng m = 20 g, đặt trên giá đỡ nằm ngang. Hệ số ma sát giữa vật và giá đỡ là \(\mu = 0,1\). Lấy g = 10 m/s². Từ VTCB đưa vật về vị trí lò xo dãn 10 cm rồi buông cho vật dao động tắt dần. Tìm v_max?
Giải:
k = 1 N/m; m = 20 g = 0,02 kg
\(\mu = 0,1\); g = 10 m/s²
A = 10 cm = 0,1 m
v_max = ?
\(F_{dh} = F{ms} \Rightarrow kx_0 = \mu mg \Rightarrow x_0 = \frac{\mu mg}{k}\)
\(\Rightarrow x_0 = \frac{0,1.0,02.10}{1} = 0,02\ m\)
\(\Rightarrow v_{max} = \sqrt{\frac{k}{m}}(A - x_0) = \sqrt{\frac{1}{0,02}}(0,1 - 0,02) = 0,4 \sqrt{2} \ (m/s)\)

VD2: Một con lắc đơn có chiều dài ℓ, vật nặng m, gia tốc g. Từu VTCB đưa vật về vị trí có phương dây treo hợp với phương thẳng đứng 1 góc \(\alpha _0\) rồi buông cho vật dao động. Trong quá trình dao động vật luôn chịu tác dụng của lực cản F_c không đổi. Tìm v_max?
Giải:
\(\cdot \ \omega = \sqrt{\frac{g}{\ell}}\)
\(\cdot \ S_0 = \alpha _0.\ell;\ x_0 = \frac{F_c}{m\omega ^2}\)
\(\Rightarrow x_0 = \frac{F_c}{m.\frac{g}{\ell}} = \frac{\ell.F_c}{mg}\)
\(\Rightarrow v_{max} = \omega (S_0 - x_0) = \sqrt{\frac{g}{\ell}}.\left ( \alpha _0.\ell - \frac{\ell.F_c}{mg} \right )\)
\(\Rightarrow v_{max} = \sqrt{\frac{g}{\ell}}.\ell \left ( \alpha _0- \frac{F_c}{mg} \right )\)
Vậy: \(v_{max} = \sqrt{g.\ell} \left ( \alpha _0- \frac{F_c}{mg} \right )\)