GIỚI THIỆU BÀI HỌC
Bài học hướng dẫn học sinh thành lập phương trình dao động điều hòa của vật. Qua đó áp dụng phương trình dao động điều hòa tìm các đại lượng A, ⍵,...
NỘI DUNG BÀI HỌC
Những bài học trước chúng ta đã được tìm hiểu hai dạng bài tập của Dao động điều hòa. Và hôm nay chúng ta tiếp tục tìm hiểu dạng tiếp theo là Viết phương trình dao động của vật.
Phương trình dao động điều hòa có dạng
\(x = A.cos(\omega t + \varphi )\)
* Tìm A:
\(\cdot \ A = \frac{\ell_{max} - \ell_{min}}{2} = \frac{\ell}{2}\)
\(\cdot \ A = \frac{v_{max}}{\omega } = \frac{a_{max}}{\omega ^2} = \sqrt{x^2 + \left ( \frac{v}{\omega } \right )^2}\)
* Tìm \(\omega\): \(\omega = \frac{2\pi}{T} = 2\pi f\)
· Vật thực hiện được n dao động trong thời gian ∆t ⇒ \(T = \frac{\Delta t}{n}\)
* Tìm \(\varphi\):
+ Tại \(t = 0: \left\{\begin{matrix} x = x_0\\ v_0\ ? \ \ \ \end{matrix}\right. \Rightarrow \left\{\begin{matrix} x_0 = A.cos (\omega .0 + \varphi )\\ sin(\omega .0 + \varphi ) \hspace{1,4cm} \end{matrix}\right.\)
NHỚ: v0 trái dấu với \(sin(\omega .0 + \varphi )\)
\(\Rightarrow \left\{\begin{matrix} cos \varphi = \frac{x_0}{A} \Rightarrow \varphi = \pm \varphi _0\\ sin\varphi ?\Rightarrow Chon\ \varphi _0 \ \ \ \ \ \end{matrix}\right.\)
+ Tại t = t0:
- \(x_0 = A.cos(\omega t + \varphi )\)
- v0 (v0 trái dấu với \(sin(\omega t + \varphi )\))
VD1: Một vật dao động điều hòa trên quỹ đạo 16 cm. Trong \(\frac{2}{3}\) phút vật thực hiện được 40 dao động. Chọn gốc tọa độ tại VTCB, gốc thời gian là lúc vật có li độ \(4\sqrt{3}\)(cm) và đang ra xa VTCB. Viết phương trình dao động?
Giải:
\(\cdot \ \ell = 16cm \rightarrow A = \frac{\ell }{2} = 8cm\)
\(\cdot \ \left\{\begin{matrix} n = 40\ dao \ dong\\ \Delta t = \frac{2}{3}\ phut = 10s \end{matrix}\right. \Rightarrow T = \frac{\Delta t}{n} = 1s\)
\(\Rightarrow \omega = \frac{2\pi}{T} = 2 \pi (\frac{rad}{s})\)
\(t = 0 \left\{\begin{matrix} x = 4\sqrt{3} \hspace{2,5cm}\\ ra \ xa \ VTCB \Rightarrow v > 0 \end{matrix}\right.\)
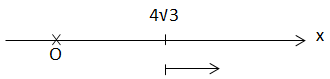
\(\Rightarrow \left\{\begin{matrix} 4\sqrt{3} = 8.cos \varphi \\ v>0 \hspace{1,6cm} \end{matrix}\right. \Rightarrow \left\{\begin{matrix} cos \varphi = \frac{\sqrt{3}}{2}\\ sin \varphi < 0 \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} cos \varphi = cos \left ( \frac{\pi}{6} \right ) \Rightarrow \varphi = \pm \frac{\pi}{6}\\ sin \varphi < 0 \Rightarrow Chon\ \varphi = -\frac{\pi}{6} \end{matrix}\right.\)
Vậy \(x = 8.cos (2\pi t - \frac{\pi}{6})(cm)\)
VD2: Một vât dao động điều hòa với tần số 2Hz. Tại thời điểm \(\frac{1}{12}\)s vật có li độ -2,5 cm và vận tốc \(-10\pi \sqrt{3} \ \frac{cm}{s}\). Viết phương trình dao động?
Giải:
\(\cdot \ f = 2Hz \Rightarrow \omega = 2 \pi f = 4 \pi \frac{rad}{s}\)
\(\cdot \ t = \frac{1}{12}s \left\{\begin{matrix} x= -2,5 cm\\ v = -10 \pi \sqrt{3}\frac{cm}{s} \end{matrix}\right.\)
\(A = \sqrt{x^2 + \left ( \frac{v}{\omega } \right )^2}\)
\(\Rightarrow A = \sqrt{(-2,5)^2 + \left ( \frac{-10\pi \sqrt{3}}{4 \pi } \right )^2} = 5 cm\)
\(\cdot \ t = \frac{1}{12}s \left\{\begin{matrix} x = -2,5\\ v < 0 \ \ \ \ \ \end{matrix}\right.\Rightarrow \left\{\begin{matrix} -2,5 = 5coss(4\pi . \frac{1}{12} + \varphi )\\ v < 0 \hspace{3,5cm} \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} cos(4 \pi \frac{1}{12} + \varphi ) = - \frac{1}{12}\\ sin (4 \pi \frac{1}{12} + \varphi ) > 0 \ \ \ \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} cos( \frac{\pi}{3} + \varphi ) = cos (\frac{2\pi}{3})\\ sin (\frac{\pi}{3} + \varphi ) > 0 \ \ \ \ \ \ \ \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \frac{\pi}{3} + \varphi = \pm \frac{2\pi}{3} \ \ \ \\ sin (\frac{\pi}{3} + \varphi ) > 0 \end{matrix}\right. \Rightarrow \frac{\pi}{3} + \varphi = \frac{2\pi}{3}\)
\(\Rightarrow \varphi = \frac{\pi}{3}\)
Vậy PTDĐ: \(x = 5.cos(4 \pi t + \frac{\pi}{3})\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



