GIỚI THIỆU BÀI HỌC
Hôm nay chúng ta tiếp tục qua dạng bài tập thứ 3 của Hiện tượng quang điện, đây cũng là một trong các ứng dụng quan trọng của hiện tượng quang điện ngoài :Chuyển động của electron trong từ trường đều. Mời các em cùng tìm hiểu .
NỘI DUNG BÀI HỌC
* Xét electron quang điện chuyển động với vận tốc \(\overrightarrow{v_0}\) trong vùng từ trường đều \(\overrightarrow{B}\ (\overrightarrow{B} \perp \overrightarrow{v_0})\)
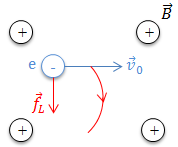
Electron quang điện chịu tác dụng của lực Lorenzt \(\overrightarrow{f}_L\), \(\overrightarrow{f}_L\) không sinh công mà đóng vai trò là lực hướng tâm làm electron chuyển động tròn đều
\(\Rightarrow f_L = F_{ht} \Rightarrow |e|.v_0.B = m.\frac{v_{0}^{2}}{R}\)
\(\Rightarrow R = \frac{mv_0}{|e|.B}\) Với \(\left\{\begin{matrix} m = m_e = 9,1.10^{-31}\ kg\\ |e| = 1,6.10^{-19}\ C \hspace{1,2cm} \end{matrix}\right.\)
Nếu \(v_{0\ max} \Rightarrow R_{max} = \frac{m.v_{0\ max}}{|e|.B}\)
* Chú ý: Nếu \(\overrightarrow{v}\) xiên góc với \(\overrightarrow{B}\)
\(\Rightarrow R = \frac{m.v_n}{|e|.B},\ \overrightarrow{v_n} \perp \overrightarrow{B}\)
Lúc này quỹ đạo là đường xoắn ốc
* Nếu electron chuyển động trong điện trường đều \(\overrightarrow{E}\) ⇒ Electron chịu tác dụng của lực điện trường \(\overrightarrow{F} = -|e|\overrightarrow{E}\)
Sử dụng định lý động năng: \(\Delta E_d = E_{d_1} - E_{d_2} = A_{\overrightarrow{F_{dt}}}\)
VD1: Chiếu một bức xạ đơn sắc có bước sóng \(\lambda\) vào tấm kim loại có giới hạn quang điện \(\lambda _0 = 2\lambda\). Các quan electron vừa bay ra được hướng vào vùng từ trường đều \(\overrightarrow{B} \perp \overrightarrow{v}\). Xác định biểu thức tính bán kính quỹ đạo của electron?
Giải:
Vận tốc quang electron: v0 max
\(R_{max} = \frac{m.v_{0\ max}}{|e|.B}\)
Mà: \(v_{0\ max} = \sqrt{\frac{2hc}{m}.\left ( \frac{1}{\lambda } - \frac{1}{\lambda _0} \right )} = \sqrt{\frac{2hc}{m.\lambda _0}}\)
\(\Rightarrow R_{max} = \frac{m}{|e|.B}. \sqrt{\frac{2hc}{m.\lambda _0}} = \frac{1}{|e|.B}. \sqrt{\frac{2hcm}{\lambda _0}}\)
VD2: Chiếu một bức xạ đơn sắc có \(\lambda =0,2 \ \mu m\) vào một tám kẽm có giới hạn quang điện \(\lambda _0 = 0,35 \ \mu m\). Electron vừa bật ra được hướng vào điện trường đều có độ lớn E = 400 V/m (\(\overrightarrow{E}\) cùng hướng \(\overrightarrow{v}\)). Tìm quãng đường electron đi được trong điện trường?
Giải:
Eđo max = \(\frac{hc}{\lambda } - \frac{hc}{\lambda _0}\)
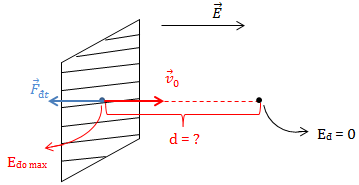
Ta có: Eđ - Eđo max = AFđt = -|e|.E.d
⇒ 0 - Eđo max = -|e|.E.d
⇒ 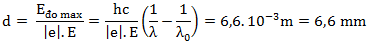














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



