Dạng 4: Khảo sát công suất

Hôm nay chúng ta học dạng 4: Khảo sát công suất, đây là dạng cuối cùng của bài Công suất. Thực ra dạng bài này là tổng hợp các dạng trên và thông qua nó, các em sẽ có cái nhìn toàn diện hơn về công suất. Công suất sẽ thay đổi thế nào khi một đại lượng thay đổi? Cực đại ở đâu? Khi đại lượng đó tiến ra vô cùng hay bằng 0 thì như thế nào?

Trong dạng bài khảo sát công suất này, chúng ta không thể làm tỉ mỉ như toán học, mà chúng ta chỉ lấy những giá trị đặc biệt như sau: 

* Khảo sát P theo R: \(P = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2}\)
\(\\ \cdot \ R = 0 \Rightarrow P = 0\\ \cdot \ R = R_0: R_0 = |Z_L - Z_C| \rightarrow P_{max} = \frac{U^2}{2R_0}=\frac{U^2}{2|Z_L - Z_C|} \\ \cdot \ R \rightarrow \infty \Rightarrow P = 0\)
* Đồ thị:
\(\left\{\begin{matrix} R_1 + R_2 = \frac{U^2}{P} \hspace{1,2cm}\\ R_1.R_2 = (Z_L - Z_C)^2 \end{matrix}\right.\)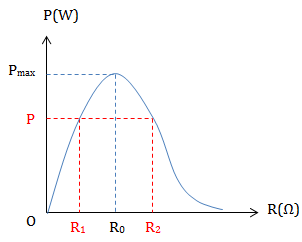     

\(R_1.R_2 = R_{0}^{2}\)

* Khảo sát P theo C: \(P = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2}\)
\(\\ \cdot \ C = 0 \Rightarrow Z_C = \infty \Rightarrow P = 0 \\ \cdot \ C=C_0: Z_{C_0} = Z_{L} \Rightarrow P_{max} = \frac{U^2}{R}\\ \cdot \ C \rightarrow \infty \Rightarrow Z_C \rightarrow 0 \Rightarrow P \rightarrow P_0 = R.\frac{U^2}{R^2 + Z_{L}^{2}}\)
* Đồ thị:
\(Z_{C_1} + Z_{C_2} = 2Z_{L}\)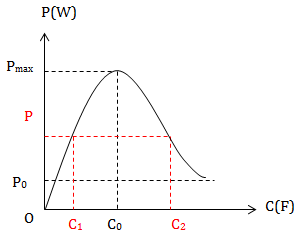     

\(Z_{C_1} + Z_{C_2} = 2Z_{C_0} \Leftrightarrow \frac{1}{C_1} + \frac{1}{C_2} = \frac{2}{C_0}\)

* Khảo sát P theo L: \(P = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2}\)
\(\\ \cdot \ L = 0 \Rightarrow Z_L = 0 \Rightarrow P = P_1 = R.\frac{U^2}{R^2 + Z_{C}^{2}} \\ \cdot \ L=L_0: Z_{L_0} = Z_{C} \Rightarrow P_{max} = \frac{U^2}{R}\\ \cdot \ L \rightarrow \infty \Rightarrow Z_L \rightarrow \infty \Rightarrow P =0\)
* Đồ thị:
\(Z_{L_1} + Z_{L_2} = 2Z_{C}\)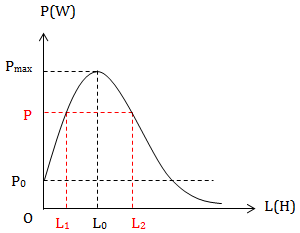     

\(Z_{L_1} + Z_{L_2} = 2Z_{L_0} \Leftrightarrow L_1 + L_2 = 2L_0\)

* Khảo sát P theo \(\omega\): \(P = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2}\)
\(\\ \cdot \ \omega = 0\Rightarrow \left\{\begin{matrix} Z_L = 0\\ Z_C = \infty \end{matrix}\right. \Rightarrow P = 0\\ \cdot \ \omega = \omega _0: Z_{L_0} = Z_{C_0} \Rightarrow omega _0 = \frac{1}{\sqrt{LC}} \Rightarrow P_{max} = \frac{U^2}{R} \\ \cdot \ \omega \rightarrow \infty \Rightarrow \left\{\begin{matrix} Z_L \rightarrow \infty \\ Z_C \rightarrow 0 \ \end{matrix}\right. \Rightarrow P \rightarrow 0\)
* Đồ thị:
\(\omega _1.\omega _2 = \omega _{0}^{2}\)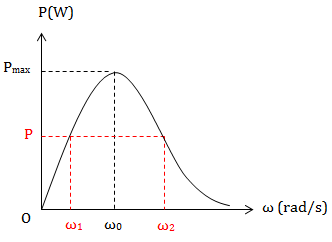     

VD1: Đặt điện áp \(u = U\sqrt{2}\cos 100 \pi t\) (V) vào 2 đầu mạch RLC ghép nối tiếp có \(L = \frac{2}{5 \pi }\ H; \ C = 31,8\ \mu F\), điện trở R thay đổi được. Khi cho R tăng từ 30 \(\Omega\) đến 50 \(\Omega\) thì công suất thay đổi như thế nào?
Giải:
\(\\ Z_L = L \omega = \frac{2}{5 \pi } .100 \pi = 40 \ \Omega \\ Z_C = \frac{1}{C \omega } = \frac{1}{31,8.10^{-6}.100 \pi} = 100\ \Omega \\ P_{max} \Rightarrow R_0 = |Z_L - Z_C| = 60\ \Omega\)
Vì \(30 < 50 < R_0 = 60 \ \Omega\) ⇒ Công suất tiêu thụ của mạch luôn tăng.

VD2: Đặt điện áp \(u = U_0\cos 100\pi t\) (V)vào 2 đầu mạch RLC ghép nối tiếp có R = 100 \(\Omega\) và tụ C thay đổi được. Khi \(C = C_1 = \frac{10^{-4}}{2 \pi }\ F\) hoặc \(C = C_2 = \frac{10^{-4}}{4 \pi }\ F\) thì mạch tiêu thụ cùng công suất; khi C = C₀ thì P_max = 200 W. Tìm các giá trị C₀, L, U₀?

Giải:
Ta có: \(\frac{1}{C_1} + \frac{1}{C_2} = \frac{2}{C_0} \Rightarrow C_0 = \ ?\)
\(\\ Z_{C_1} = \frac{1}{C_1\omega } = \frac{1}{\frac{10^{-4}}{2 \pi }.100 \pi } = 200\ \Omega \\ Z_{C_2} = \frac{1}{C_2\omega } = \frac{1}{\frac{10^{-4}}{4 \pi }.100 \pi } = 400\ \Omega \\ \cdot \ Z_L = Z_{C_0} = \frac{Z_{C_1} + Z_{C_2}}{2} = 300\ \Omega \\ \left\{\begin{matrix} \cdot \ L = \frac{Z_L}{\omega } = \frac{300}{100 \pi } = \frac{3}{\pi }\ (H) \hspace{1,5cm}\\ \cdot \ C_0 = \frac{1}{Z_{C_0}\omega } = \frac{1}{300.100\pi } = \frac{10^{-4}}{3 \pi }\ (F) \end{matrix}\right.\\ \cdot \ P_{max} = \frac{U^2}{R} = 200 \Rightarrow U^2 = 200.100 = 2.10^4\\ \Rightarrow U = 100\sqrt{2} \ (V) \\ \Rightarrow U_0 = U\sqrt{2} = 200 \ (V)\)