Dạng 1: Cắt - Ghép lò xo

Bài học này giúp học sinh nắm được công thức tính độ cứng lò xo, các công thức biến đổi khi cắt, ghép lò xo (ghép nối tiếp, ghép song song). Qua đó có thêm công cụ tính độ cứng, xét tính ⍵ của các lò xo, có thêm công thức giải được nhiều bài toán.

Chúng ta tìm hiểu dạng đầu tiên của con lắc lo xo là Cắt - Ghép lò xo.

Ở dạng này các em cần chú ý, trong đề thi những câu rơi vào dạng này thường là những câu khó, nhưng nếu các em không biết thì rất là tiếc, bời vì nó sẽ khó với những bạn không biết và sẽ không khó với những bạn đã ôn tập.

* Cắt lò xo

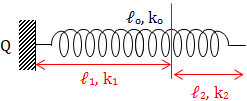
Ta có:
\(\left.\begin{matrix} \cdot \ k_0 = \frac{E.S}{\ell _0}\\ \cdot \ k_1 = \frac{E.S}{\ell _1}\\ \cdot \ k_2 = \frac{E.S}{\ell _2} \end{matrix}\right\} k_0. \ell _0 = k_1. \ell _1 = k_2. \ell _2 = ... =\) hằng số
⇒ Độ cứng k của lò xo tỉ lệ nghịch với chiều dài ℓ của nó

* Ghép lò xo
+ Ghép song song

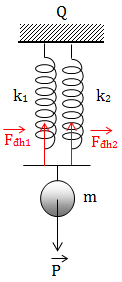
Tại vị trí cân bằng
\(\overrightarrow{P} + \underbrace{ \overrightarrow{F}_{dh_1} + \overrightarrow{F}_{dh_2}}_{\overrightarrow{F}_{dh}} = \overrightarrow{O}\)
Vì \(\Delta \ell _1 = \Delta \ell _2 = \Delta \ell\)
\(\Rightarrow k. \Delta \ell = k_1. \Delta \ell _1 + k_2. \Delta \ell _2\)
\(\Rightarrow k_{//} = k_1+k_2, \ k_{//} > k_1,k_2\)

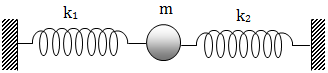
\(\Rightarrow k_{//} = k_1+k_2\)
+ Ghép nối tiếp

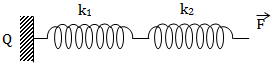
Ta có: \(x = x_1 + x_2\)
Mà:
\(\left.\begin{matrix} x_1 = \frac{F_{dh_1}}{k_1}\\ x_2 = \frac{F_{dh_2}}{k_2}\\ x = \frac{F}{k} \ \ \ \ \end{matrix}\right\}\) Mà: \(F = F_{dh_1} = F_{dh_2} \Rightarrow x = x_1+x_2 \Rightarrow \frac{1}{k_{nt}} = \frac{1}{k_1} + \frac{1}{k_2}\)
\(\Rightarrow k_{nt} = \frac{k_1.k_2}{k_1 + k_2} < k_1, k_2\)

VD1: Một lò xo có chiều dài ℓ₀, độ cứng 120 N/m. Cắt lò xo thành 2 đoạn \(\ell _1 = \frac{3}{8} \ell _0\) và ℓ₂ độ cứng tương ứng là k₁, k₂. Tìm k₁, k₂?
Giải:
\(\\ k_0 = 120 \ N/m, \ell _1 = \frac{3}{8} \ell _0\\ \ell _1 + \ell _2 = \ell _0 \Rightarrow \ell _2 = \frac{5}{8} \ell _0\)
Ta có: \(\left\{\begin{matrix} k_1 \ell _1 = k_0 \ell _0 \Rightarrow k_1 = \frac{k_0 \ell _0}{\ell _1} = 120.\frac{8}{3} = 320 \ (N/m) \\ k_2 \ell _2 = k_0 \ell _0 \Rightarrow k_2 = \frac{k_0 \ell _0}{\ell _2} = 120.\frac{8}{5} = 192\ (N/m) \end{matrix}\right.\)

VD2: Một lò xo có độ cứng 60 N/m, nếu cắt lò xo thành 2 phần có chiều dài bằng nhau rồi mang ghép song song lại với nhau thì được 1 lò xo có độ cứng bao nhiêu?
Giải:
\(\\ \ell _1 = \ell _2 = \frac{\ell _0}{2} \Rightarrow k_1 = k_2 = 2k_0\\ \Rightarrow k_1 = k_2 = 2.60 = 120 \ (N/m)\\ \Rightarrow k_{//} = k_1 + k_2 = 240 \ (N/m)\)