Dạng 5: Bài toán cực trị

Chúng ta tiếp tục học dạng 5: Bài toán cực trị, đây là dạng bài độc lập với công suất, nó như 1 bài toán tổng hợp của điện xoay chiều. Thực chất đó chính là cách giải bài toán bằng chữ sau đó gặp những bài toán bằng số, chúng ta sẽ nhớ lại cách đã trình bày, quá trình mình đi đến kết quả cuối cùng như thế nào. Và tốt hơn hết, với dạng này các em nên nhớ các công thức được đóng khung cuối cùng.

* Thay đổi L để U_L lớn nhất

Ta có: \(U_L = I.Z_L = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_L = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{L}^{2}}}}\)
\(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2+Z_{L}^{2}-2Z_LZ_C+Z_{C}^{2}}{Z_{L}^{2}}}} = \frac{U}{\sqrt{\frac{R^2+Z_{C}^{2}}{Z_{L}^{2}}-2\frac{Z_C}{Z_L}+1}} = \frac{U}{\sqrt{y}}\)
Với \(\left\{\begin{matrix} y=(R^2 + Z_{C}^{2}).x^2 - 2Z_C.x + 1\\ x=\frac{1}{Z_L} \hspace{4,2cm} \end{matrix}\right.\)   \(\left ( \begin{matrix} y = ax^2 + bx+ c\\ \left\{\begin{matrix} a = R^2 + Z_{C}^{2}\\ b=-2Z_C \ \ \ \ \\ c=1 \ \ \ \ \ \ \ \ \ \ \end{matrix}\right. \end{matrix} \right )\)
Do U không đổi \(\Rightarrow (U_L)_{max} \Leftrightarrow y_{min} \Rightarrow x = -\frac{b}{2a}\)
\(\Rightarrow \frac{1}{Z_L}=\frac{Z_C}{R^2 + Z_{C}^{2}} \Rightarrow Z_L=\frac{R^2 + Z_{C}^{2}}{Z_C} \Rightarrow U_{L\ max} = \frac{U}{R}\sqrt{R^2 + Z_{C}^{2}}\)
* Giản đồ vecto

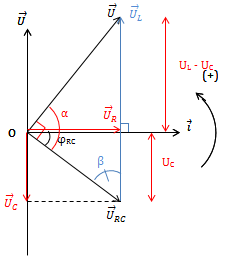
Ta có: \(\frac{U_L}{\sin \alpha } = \frac{U}{\sin \beta } \Rightarrow U_L = \frac{U}{\sin \beta }.\sin \alpha\)
Do U, \(\beta\) không đổi \(\Rightarrow U_{L\ max} \Leftrightarrow \sin \alpha = 1 \Rightarrow \alpha = \frac{\pi }{2}\)
\(\cdot \ \overrightarrow{U}_{RC} \perp \overrightarrow{U} \Rightarrow U_{RC}^{2} = U_C.U_L \Rightarrow Z_{RC}^{2} = Z_C.Z_L \Rightarrow Z_L = \frac{R^2 + Z_{C}^{2}}{Z_C}\)
\(\cdot \ U_{RC}.U = U_{R}.U_{L} \Rightarrow U_{L} = \frac{U}{U_R}.U_{RC}\)
\(\cdot \ U_{R}^{2}= U_{C}(U_{L}-U_{C})\)
\(\cdot \ U^{2}= (U_{L}-U_{C}).U_{L}\)
   \(U_{L}^{2}= U^2 + U_{RC}^{2}\)
\(\Rightarrow U_{L}^{2}= U^2 + U_{R}^{2} + U_{C}^{2}\)

* Thay đổi C để U_C lớn nhất
Ta có: \(U_C = I.Z_C = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_C = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{C}^{2}}}}\)
\(\Rightarrow U_C = \frac{U}{\sqrt{\frac{R^2+Z_{L}^{2}}{Z_{C}^{2}}-2\frac{Z_L}{Z_C}+1}} = \frac{U}{\sqrt{y}}\)
Với \(\left\{\begin{matrix} y=(R^2 + Z_{L}^{2}).x^2 - 2Z_L.x + 1 \ \ \ (y = ax^2 + bx + c)\\ x=\frac{1}{Z_C} \hspace{8cm} \end{matrix}\right.\)
Do U không đổi \(\Rightarrow U_{c\ max} \Leftrightarrow y_{min} \Rightarrow x = -\frac{b}{2a}\)
\(\Rightarrow \frac{1}{Z_C}=\frac{Z_L}{R^2 + Z_{L}^{2}} \Rightarrow Z_C=\frac{R^2 + Z_{L}^{2}}{Z_L} \Rightarrow U_{C\ max} = \frac{U}{R}\sqrt{R^2 + Z_{L}^{2}}\)

* Thay đổi C để U_{C max} (Giản đồ vecto)

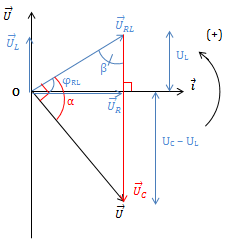
Ta có: \(\frac{U_C}{\sin \alpha } = \frac{U}{\sin \beta } \Rightarrow U_C = \frac{U}{\sin \beta }.\sin \alpha\)
Do U, \(\beta\) không đổi \(\Rightarrow U_{C\ max} = \frac{U}{\sin \beta }\) khi \(\sin \alpha =1 \Rightarrow \alpha =\frac{\pi}{2}\)
\(\cdot \ \overrightarrow{U}_{RL} \perp \overrightarrow{U} \Rightarrow U_{RL}^{2} = U_L.U_C \Rightarrow Z_{RL}^{2} = Z_L.Z_C\)
\(\Rightarrow Z_C = \frac{R^2 + Z_{L}^{2}}{Z_L}\)
\(\cdot \ U.U_{RL} = U_{R}.U_{C} \Rightarrow U_{C} = \frac{U}{U_{R}}.U_{RL} = \frac{U}{R}.\frac{U_{RL}}{I}\)
\(\Rightarrow U_{C} = \frac{U}{R}.Z_{RL}=\frac{U}{R}\sqrt{R^2 + Z_{L}^{2}}\)
* Chú ý:
(1) Thay đổi C thấy có 2 giá trị C₁, C₂ thì U_C1 = U_C2; khi C = C₀ thì U_{C max}:
\(\Rightarrow x_1 + x_2 = -\frac{b}{a} = 2x_0 \Rightarrow \frac{1}{Z_{C_1}} + \frac{1}{Z_{C_2}} = \frac{2}{Z_{C_0}}\)
⇒ C₁ + C₂ = 2C₀
(2) Thay đổi C để:
\(\\ + \ U_{R \ max} = U\\ + \ U_{L \ max} = \frac{U}{R}.Z_L\\ + \ U_{RL \ max} = \frac{U}{R}.Z_{RL}\)
⇒ Cộng hưởng điện.

* Thay đổi \(\omega\) để U_L max
Ta có: \(U_L = I.Z_L = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_L = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{L}^{2}}}}\)
\(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2}{Z_{L}^{2}}+\left ( 1-\frac{Z_C}{Z_L} \right )^2}} = \frac{U}{\sqrt{\frac{R^2}{L\omega ^2}+\left ( 1-\frac{1}{LC\omega ^2} \right )^2}}\)
\(\Rightarrow U_L = \frac{U}{\sqrt{\frac{R^2}{L^2 \omega ^2}+1-\frac{2}{LC \omega ^2}+\frac{1}{L^2C^2 \omega ^4}}} = \frac{U}{\sqrt{\frac{1}{L^2C^2 \omega ^4}-\left ( \frac{2}{LC}-\frac{R^2}{L^2} \right )\frac{1}{\omega ^2}+1}}\)
\(\Rightarrow U_L = \frac{U}{\sqrt{y}}\) với \(\left\{\begin{matrix} y = \frac{1}{L^2C^2}.x^2 - \left ( \frac{2}{LC} - \frac{R^2}{L^2} \right ).x + 1\\ x = \frac{1}{\omega ^2} \hspace{4,6cm} \end{matrix}\right.\)
Do U không đổi \(\Rightarrow (U_L)_{max} \Leftrightarrow y_{min} \Leftrightarrow x = -\frac{b}{2a}\)
\(\Rightarrow \frac{1}{\omega ^2} = \frac{\frac{2}{LC}-\frac{R^2}{L^2}}{\frac{2}{L^2C^2}} = \left ( \frac{2}{LC}-\frac{R^2}{L^2} \right ).\frac{L^2C^2}{2}\)
\(\Rightarrow \frac{1}{\omega ^2} = \frac{2LC - R^2C^2}{2} \Rightarrow \omega _L = \sqrt{\frac{2}{2LC - R^2C^2}}\)
\(2LC - R^2C^2 > 0\Leftrightarrow CR^2 < 2L\)
* Chú ý: Thay đổi \(\omega\) có 2 giá trị \(\omega _1, \omega _2\) thì \(U_{L_1} = U_{L_2}\); khi \(\omega = \omega _L\) thì U_L max \(\Rightarrow x_1 + x_2 = -\frac{b}{a} = 2x_L \Rightarrow \frac{1}{\omega _{1}^{2}} +\frac{1}{\omega _{2}^{2}} = \frac{2}{\omega _{L}^{2}}\)

* Thay đổi \(\omega\) để U_C max
Ta có: \(U_C = I.Z_C = \frac{U}{\sqrt{R^2 + (Z_L - Z_C)^2}}.Z_C = \frac{U}{\sqrt{\frac{R^2 + (Z_L - Z_C)^2}{Z_{C}^{2}}}}\)
\(\Rightarrow U_C = \frac{U}{\sqrt{\frac{R^2}{Z_{C}^{2}}+\left ( \frac{Z_L}{Z_C}-1 \right )^2}} = \frac{U}{\sqrt{R^2C^2\omega ^2+(LC\omega ^2 - 1)^2}}\)
\(\Rightarrow U_C = \frac{U}{\sqrt{R^2C^2\omega ^2 + L^2C^2\omega ^4 - 2LC\omega ^2 + 1}}\)
             \(= \frac{U}{\sqrt{L^2C^2\omega ^4 - (2LC - R^2C^2)\omega ^2 + 1}} = \frac{U}{\sqrt{y}}\)
Với \(\left\{\begin{matrix} y = L^2C^2x^2 - (2LC - R^2C^2)x + 1\\ x = \omega ^2 \hspace{5cm} \end{matrix}\right.\)
Do U không đổi \(\Rightarrow U_{C\ max} \Leftrightarrow y_{min} \Rightarrow x = \frac{-b}{2a}\)
\(\Rightarrow \omega ^2 = \frac{2LC - R^2C^2}{2L^2C^2} \Rightarrow \omega _C = \frac{1}{LC}.\sqrt{\frac{2LC - R^2C^2}{2}}\)
* Chú ý: Thay đổi \(\omega\) có 2 giá trị \(\omega _1, \omega _2\) thì \(U_{C_1} = U_{C_2}\); khi \(\omega = \omega _C\) thì U_C max
\(\Rightarrow x_1 + x_2 = 2x_C \Rightarrow \omega _{1}^{2} + \omega _{2}^{2} = 2\omega _{C}^{2}\)
Nhận xét:
\(\cdot \ \omega _{0}^{2} = \frac{1}{LC}\) (CHĐ)
\(\cdot \ \omega _{C} = \frac{1}{LC}.\sqrt{\frac{2LC - R^2C^2}{2}}\)
\(\cdot \ \omega _{L} = \sqrt{\frac{2}{2LC - R^2C^2}}\)
Ta có mối liên hệ \(\Rightarrow \omega _C \omega _L = \omega _{0}^{2}\)

VD1: Đặt điện áp \(u = 200\sqrt{2}\cos 100 \pi t\) (V) vào 2 đầu mạch RLC ghép nối tiếp có L thay đổi được. Thay đổi L để U_{L max} = 250 V thì U_R bằng bao nhiêu?
Giải:

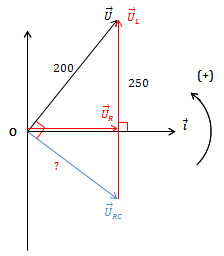
\(\cdot \ U_{RC} = \sqrt{U_{L}^{2} - U^2} = \sqrt{250^{2} - 200^2} \Rightarrow U_{RC} = 150 \ V\)
\(\cdot \ U_{R} = \frac{U.U_{RC} }{U_L} = \frac{200.150}{250} = 120\ V\)

VD2: Đặt điện áp \(u = 100\sqrt{2}\cos (100 \pi t - \frac{\pi }{3})\) (V) vào 2 đầu mạch gồm \(R = 50\Omega\) nối tiếp cuộn dây chỉ có \(L = \frac{2}{5 \pi }\) (H) và tụ C thay đổi được. Thay đổi C để điện áp hiệu dụng 2 đầu cuộn dây lớn nhất bằng bao nhiêu?
Giải:
Thay đổi C để \(U_{L\ max} = \frac{U}{R}.Z_L\)
Với \(\left\{\begin{matrix} U = 100 \ V \hspace{2,8cm}\\ R = 50\Omega \hspace{3,2cm}\\ Z_L = L \omega =\frac{2 \pi}{5}.100\pi = 40\Omega \end{matrix}\right.\)
\(\Rightarrow U_{L\ max} = \frac{100}{50}.40 = 80\ V\)