GIỚI THIỆU BÀI HỌC
Qua bài giảng video Sóng dừng này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
-
Trình bày được bản chất của sự phản xạ sóng.
-
Nắm được định nghĩa sóng dừng.
-
Vận dụng công thức để hoàn thành bài tập
NỘI DUNG BÀI HỌC
Hôm nay chúng ta qua bài số 3: Sóng dừng. Nghiên cứu sóng dừng là gì? Và thực ra nó không xa lạ với chúng ta.
1. Phản xạ sóng
Khi sóng truyền đi nếu gặp vật cản thì nó sẽ bị phản xạ. Sóng phản xạ luôn cùng tần số và tốc độ truyền sóng với sóng tới.
+ Vật cản cố định:

⇒ Sóng phản xạ và sóng tới luôn ngược pha tải điểm phản xạ
+ Vật cản tự do:

⇒ Sóng phản xạ luôn cùng pha với sóng tới tại điểm phản xạ.
2. Phương trình sóng dừng
Xét sợi dây có chiều dài ℓ, đầu A dao động với phương trình \(u_A = a\cos \omega t\); đầu B cố định
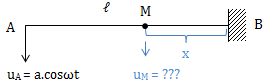
Sóng tại M và B do A truyền đến:
\(\left\{\begin{matrix} u_{AM} = a\cos (\omega t - \frac{2 \pi (\ell - x)}{\lambda })\\ u_{AB} = a \cos (\omega t - \frac{2 \pi \ell}{\lambda }) \ \ \ \ \ \end{matrix}\right.\)
Sóng phản xạ tại B:
\(u_B = - u_{AB} = - a \cos (\omega t - \frac{2 \pi \ell}{\lambda })\)
\(u_B = a \cos (\omega t - \frac{2 \pi \ell}{\lambda } + \pi )\)
Sóng tại M do B phản xạ:
\(u_{BM} = a \cos (\omega t - \frac{2 \pi \ell}{\lambda } + \pi - \frac{2 \pi.x}{\lambda })\)
⇒ Sóng tổng hợp tại M: uM = uAM + uBM
\(u_{M} = 2a\cos \left [ \frac{2 \pi x}{\lambda } - \frac{\pi }{2} \right ] \cos \left [ \omega t + \frac{\pi}{2} - \frac{2\pi \ell }{\lambda } \right ]\)
* Tại M sóng có biên độ cực đại (bụng sóng)
\(A_M = 2a \left | \cos \left ( \frac{2 \pi x}{\lambda } - \frac{\pi }{2} \right ) \right | = 2a\)
\(\Rightarrow \cos \left ( \frac{2\pi x}{\lambda } - \frac{\pi }{2}\right ) = \pm 1 \Rightarrow \frac{2\pi x}{\lambda } - \frac{\pi }{2} = k \pi\)
\(\Rightarrow x = \left ( k + \frac{1}{2} \right ) \frac{\lambda }{2} = (2k + 1) \frac{\lambda }{4}, \ \ k \in Z\)
* Tại M sóng có biên độ cực tiểu (nút sóng)
\(A_M = 0 \Rightarrow \cos \left (\frac{2\pi x}{\lambda } - \frac{\pi }{2} \right ) = 0\)
\(\Rightarrow \frac{2\pi x}{\lambda } - \frac{\pi }{2} = \left ( k - \frac{1}{2} \right ) \pi \Rightarrow x = k\frac{\lambda }{2}, \ \ \ k \in Z\)
Vậy: Sóng dừng là sự giao thoa giữa sóng tới và sóng phản xạ trên cùng một phương hay sóng dừng là sóng có các nút và bụng cố định trong không gian.
3. Hình dạng sóng dừng
* Sợi dây 2 đầu cố định
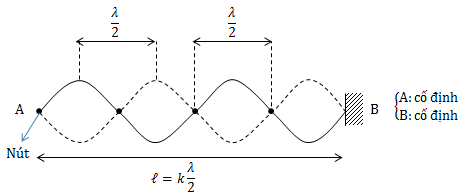
• Số bó sóng: k
• Số nút sóng: k + 1
• Số bụng sóng: k
\(\Rightarrow \lambda = \frac{2\ell }{k} \Rightarrow \lambda _{max } = 2 \ell \ (Khi \ k = 1)\)
Điều kiện để có sóng dừng: \(\ell = k.\frac{\lambda }{2}\)
* Sợi dây 1 đầu cố định, 1 đầu tự do
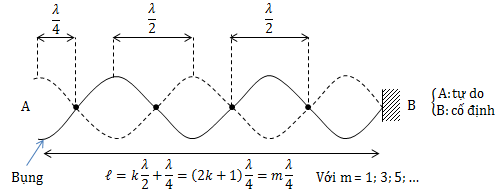
• Số bó sóng: k
• Số nút sóng: k + 1
• Số bụng sóng: k + 1
\(\lambda = \frac{4\ell}{2k + 1} \Rightarrow \lambda _{max} = 4 \ell \ (Khi \ k = 0)\)
Điều kiện để có sóng dừng: \(\ell = (2k + 1)\frac{\lambda }{4}\)
* Ứng dụng: Đo tốc độ truyền sóng
VD1: Trên sợi dây dài 2 m đang có sóng dừng với tần số 100 Hz. Người ta thấy ngoài 2 đầu dây cố định còn có 3 điểm khác luôn đứng yên. Tìm tốc độ truyền sóng?
Giải:
\(\ell = 2 \ m; \ f = 100\ Hz\)
Trên dây có 5 nút
Hai đầu có định
⇒ k = 4
\(\ell = k\frac{\lambda }{2} \Rightarrow \lambda = \frac{2 \ell}{k} = \frac{2.2}{4} = 1\ (m)\)
\(\rightarrow v = \lambda .f = 100\ m/s\)
VD2: Sợi dây AB dài 1 m, đầu A cố định, đầu B dao động với tần số thay đổi được và được xem là nút sóng. Ban đầu trên dây có sóng dừng, nếu tăng tần số thêm 30 Hz thì số nút trên dây tăng thêm 5 nút. Tìm v?
Giải:
\(\ell = 1\ m\)
Ban đầu: \(\ell = k\frac{\lambda }{2} = k = \frac{v}{2f}\)
\(\Rightarrow f = k\frac{v}{2 \ell } \ (1)\)
Nếu f + 30 và trên dây tăng 5 nút (⇒ tăng 5 bó sóng)
\(\Rightarrow f + 30 =(k + 5) \frac{v}{2 \ell }\)
\(\Leftrightarrow 30 = 5 \frac{v}{2 \ell }\)
Từ (1): \(f = k\frac{v}{2 \ell}\)
\(\Rightarrow 30 = 5\frac{v}{2 \ell} \Rightarrow v = \frac{60.1}{12}\ m/s\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



