Dạng 4: Năng lượng con lắc lò xo - Thời gian nén, dãn trong một chu kỳ

Đến với bài học này các em sẽ được củng có kiến thức, nắm vững công thức tính động năng, thế năng, cơ năng. Biết được mối liên hệ giữa cơ năng và biên độ, cách tính thời gian nén hoặc giãn trong một chu kỳ của con lắc lò xo trong các trường hợp nằm ngang, treo thẳng đứng…

Hôm nay chúng ta tiếp tục dạng 4 của bài con lắc lò xo, thực ra dạng 4 này được tách ra hai dạng, nhưng một trong hai dạng này là dạng năng lượng mà chúng ta đã làm rất nhiều ở bài dao động điều hòa nên được gộp lại với dạng bài liên quan đến thời gian nén, dãn trong một chu kỳ. Đây là dạng cuối cùng của bài con lắc lò xo.

Năng lượng của con lắc lò xo? Con lắc lò xo dao động điều hòa thì năng lượng của con lắc lò xo cũng chính là năng lượng dao động điều hòa. Nó có thêm công thức để chúng ta giải quyết bài toán. Chúng ta cũng tìm hiểu thêm về hời gian nén, dãn trong một chu kỳ mà những đề thi những năm gần đây rất hay hỏi.

* Năng lượng của con lắc lò xo
+ W_đ \(=\frac{1}{2}mv^2 = \underbrace{ \frac{1}{2}m\omega ^2A^2 }_{W}.\sin^2(\omega t + \varphi )\)
+ W_t \(=\frac{1}{2}kx^2 = \underbrace{ \frac{1}{2}k A^2 }_{W}.\cos ^2(\omega t + \varphi )\)
+ W = W_đ + W_t = \(\frac{1}{2}mv^2 + \frac{1}{2}kx^2\) (hằng số)
W = W_{đ max} = \(\frac{1}{2}mv_{max}^{2}\)
W = W_{t max} = \(\frac{1}{2}kA^2\)
Đối với con lắc lò xo thì W \(\notin\) m, W tỉ lệ với A²

* Thời gian lò xo nén, giãn trong 1 chu kỳ
+ TH: Con lắc lò xo nằm ngang

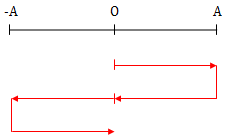
\(\Rightarrow \left\{\begin{matrix} Trong \ 1T \hspace{1,6cm}\\ \Delta t_{dan} = \Delta t_{nen} = \frac{T}{2} \end{matrix}\right.\)
+ TH: Con lắc lò xo treo thẳng đứng

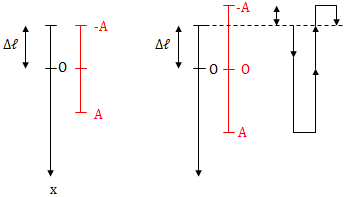
\(\cdot \ Khi\ A\leq \Delta \ell \Rightarrow \left\{\begin{matrix} Trong \ 1T\\ \Delta t_{dan} = T\\ \Delta t_{nen} = 0 \end{matrix}\right.\)
\(\cdot \ Khi\ A > \Delta \ell \Rightarrow \left\{\begin{matrix} Trong \ 1T \hspace{2,4cm} \\ \Delta t_{nen} = 2.\frac{T}{2 \pi } \cos ^{-1}\left ( \frac{\Delta \ell}{A} \right )\\ \Delta t_{dan} = T - \Delta t_{nen} \hspace{0,9cm} \end{matrix}\right.\)

* Các trường hợp đặc biệt: Con lắc lò xo treo thẳng đứng
+ TH1: \(A = 2.\Delta \ell\)
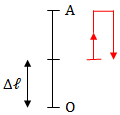 \(\Rightarrow \left\{\begin{matrix} Trong\ 1T \hspace{1,8cm}\\ \Delta t_{nen} = \frac{T}{3} \hspace{1,8cm}\\ \Delta t_{dan} = T - \frac{T}{3} = \frac{2T}{3} \end{matrix}\right.\)
+ TH2: \(A = \sqrt{2}.\Delta \ell\)
 \(\Rightarrow \left\{\begin{matrix} Trong \ 1T \hspace{2cm} \\ \Delta t_{nen} = \frac{T}{4} \hspace{1,9cm} \\ \Delta t_{dan} = T - \frac{T}{4} = \frac{3T}{4} \end{matrix}\right.\)
+ TH3: \(A = \frac{\sqrt{3}}{2}.\Delta \ell\)
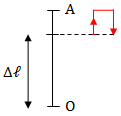 \(\Rightarrow \left\{\begin{matrix} Trong\ 1T \hspace{1,8cm} \\ \Delta t_{nen} = \frac{T}{6} \hspace{1,8cm}\\ \Delta t_{dan} = T - \frac{T}{6} = \frac{5T}{6} \end{matrix}\right.\)

Tổng quát: \(A > \Delta \ell\)
\(\left\{\begin{matrix} Trong \ 1T \hspace{2,4cm} \\ \Delta t_{nen} = 2.\frac{T}{2 \pi } \cos ^{-1}\left ( \frac{\Delta \ell}{A} \right )\\ \Delta t_{dan} = T - \Delta t_{nen} \hspace{0,9cm} \end{matrix}\right.\)

VD1: Một con lắc lò xo treo thẳng đứng có k = 100 N/m; m = 100g. Từ VTCB truyền cho vật vận tốc \(20 \pi\) cm/s để vật dao động điều hòa.
a/ Tìm W?
b/ Tìm 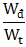 khi x = 1 cm?
c/ Tìm thời gian lò xo nén dãn trong 1 chu kỳ?
Giải:
m = 100g = 0,1kg
\(v_{max} = 20 \pi \ cm/s = 0,2 \pi \ m/s\)
a/ \(W = \frac{1}{2}mv_{max}^{2} = \frac{1}{2}.0,1.(0,2 \pi)^2 =0,02 \ J\)
b/
\(\cdot \ x = 1\ cm \Rightarrow W_t = \frac{1}{2}kx^2\)
\(\Rightarrow W_t = \frac{1}{2}.100(1.10^{-2})^2 = 5.10^{-3}\)
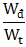⇒  \(=\frac{W - W_t}{W_t} = \frac{W}{W_t} - 1 = 3\)
\(\cdot \ \omega = \sqrt{\frac{k}{m}} = 10 \pi \Rightarrow A = \frac{v_{max}}{\omega } = 2 \ (cm)\)
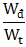⇒​  \(= \left ( \frac{A}{x} \right )^2 - 1 = 3\)
c/ \(\Delta \ell = \frac{mg}{k} = \frac{0,1.10}{100} = 0,01\ m = 1\ cm\)
\(\Rightarrow \Delta \ell = \frac{A}{2} \Rightarrow \left\{\begin{matrix} \Delta t_{nen} = \frac{T}{3} = \frac{1}{15}(s)\\ \Delta t_{dan} = \frac{2T}{3} = \frac{2}{15}(s) \end{matrix}\right.\)

VD2: Một con lắc lò xo treo thẳng đứng gồm k = 20 N/m; m = 50g. Trong 1 chu kỳ thời gian lò xo giãn gấp 2 lần thời gian lò xo nén. Tìm W?
Giải:
\(\left\{\begin{matrix} \Delta t_{dan} = 2\Delta t_{nen} \ \ \ \ \ \ \\ \Delta t_{dan} + 2\Delta t_{nen} = T \end{matrix}\right.\)
\(\Rightarrow \Delta t_{nen} = \frac{T}{3} \Rightarrow A = 2\Delta \ell\)
Ta có: \(\Delta \ell = \frac{mg}{k} = \frac{0,05.10}{20} = 0,025 \ m\)
\(\Rightarrow A = 2\Delta \ell = 0,05 \ m = 5.10^{-2} \ m\)
\(W = \frac{1}{2}k.A^2 = \frac{1}{2}20.(5-10^{-2})^2\)
\(\Rightarrow W = 25.10^{-3} \ J = 0,025 \ J\)