GIỚI THIỆU BÀI HỌC
Bài giảng cung cấp cho học sinh tìm hiểu mối liên hệ giữa các đại lượng và trạng thái của vật trong quá trình dao động. Ngoài ra nắm được các nội dung chính của bài:
- Công thức tính tần số góc.
- Khái niệm chu kỳ (T).
- Khái niệm tần số (f).
- Xác định vị trí, vận tốc, gia tốc tại thời điểm ban đầu.
- Xác định trạng thái của vật tại thời điểm ban đầu.
NỘI DUNG BÀI HỌC
Ở bài Dao động điều hòa mình chia ra thành 10 bài tập. Các dạng bài tập này cực kì quan trọng, vì trong 4 chương đầu các dạng bài tập này các em được áp dụng liên tục và cấu trúc đề thi của Bộ thì 4 chương đầu chiếm trong đề thi khoảng 6,5 điểm. Và hôm nay chúng ta bắt đầu tìm hiểu Dạng 1.
Vật dao động điều hòa có các phương trình sau: \(\left\{\begin{matrix} x = A.cos(\omega t + \varphi ) \ \ \ \ \\ v = - \omega A.sin(\omega t + \varphi )\\ a = - \omega ^2.x \hspace{2cm} \end{matrix}\right.\)
* Tần số góc ω: \(\omega = \frac{2 \pi}{T} = 2 \pi f\)
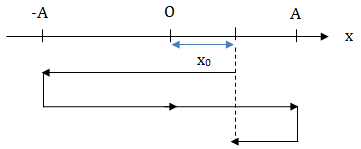
+ Chu kỳ (T): là thời gian vật thực hiện được 1 dao động hoặc là thời gian ngắn nhất mà trạng thái dao động của vật được lặp lại như cũ.
+ Tần số (f): là số dao động thực hiện được trong một đơn vị thời gian (1 giây).
* Xác định x0, v0, a0 tại thời điểm t0
Thay t = t0: \(\left\{\begin{matrix} x_0 = A.cos(\omega t_0 + \varphi ) \ \ \ \\ v_0 = - \omega A.sin(\omega t_0 + \varphi )\\ a_0 = - \omega ^2.x_0 \hspace{1,9cm} \end{matrix}\right.\)
* Chú ý: Nên đưa phương trình li độ về dạng chuẩn \(x = A.cos(\omega t + \varphi )\) trước khi các định các đại lượng.
\(\cdot \ sin(\omega t + \varphi ) =cos(\omega t + \varphi - \frac{ \pi}{2})\)
\(\cdot \ - sin(\omega t + \varphi ) =cos(\omega t + \varphi + \frac{ \pi}{2})\)
\(\cdot \ - cos(\omega t + \varphi ) =cos(\omega t + \varphi \pm \pi)\)
+ Lấy dấu (+) nếu \(\varphi < 0\)
+ Lấy dấu (-) nếu \(\varphi > 0\)
* Xác đinh trạng thái của vật tại thời điểm t0
Từ \(t = t_0 \Rightarrow \left\{\begin{matrix} x_0\\ v_0\\ a_0 \end{matrix}\right.\)
KL: Vật có li độ x0
+ Chuyển động theo chiều dương nếu v0 > 0
+ Chuyển động theo chiều âm nếu v0 < 0
+ Chuyển động nhanh dần (a0; v0 > 0)
+ Chuyển động chậm dần (a0; v0 > 0)
NHỚ: a0 luôn trái dấu với x0
VD1: Cho dao động \(x =3sin (4 \pi t + \frac{\pi}{6})\) cm
a. Xác định A, \(\omega\), T, \(\varphi\), chiều dài quỹ đạo?
b. Tìm x, v, a tại thời điểm t = 0,5s.
c. Xác định trạng thái ban đầu và trạng thái của vật tại t = 0,5s?
Giải:
\(x = 3sin(4 \pi t + \frac{\pi}{6}) = 3 cos (4 \pi t + \frac{\pi}{6} - \frac{\pi}{2})\)
\(\rightarrow x = 3cos(4 \pi t - \frac{\pi}{3}) \ (cm)\)
a.
\(A = 3\ (cm);\ \omega = 4 \pi (\frac{rad}{s});\ \varphi = - \frac{\pi }{3}\)
\(T = \frac{2 \pi }{\omega } = \frac{2 \pi }{4 \pi } = 0,5(s);\ \ell = 2A = 6\ (cm)\)
b.
Với \(x = 3cos(4 \pi t - \frac{\pi}{3})\)
\(\rightarrow \left\{\begin{matrix} v = -12 \pi .sin (4\pi t - \frac{\pi }{3})\\ a = - \omega ^2.x \hspace{2,2cm} \end{matrix}\right.\)
Tại \(t = 0,5s \Rightarrow \left\{\begin{matrix} x = 3.cos(4 \pi .0,5 - \frac{\pi }{3}) = 1,5 \ cm \ \ \ \\ v = -12 \pi .sin (4 \pi .0,5 - \frac{\pi }{3}) = 6 \pi \sqrt{3}\\ a = -(4\pi)^2.1,5 = -24 \pi ^2 \frac{cm}{s^2} \ \ \ \ \ \ \ \ \end{matrix}\right.\)
c. Trạng thái ban đầu ⇒ t = 0
Tại \(t = 0 \Rightarrow \left\{\begin{matrix} x = 3.cos(4 \pi .0 - \frac{\pi }{3}) = 1,5 \ cm \\ v = -12 \pi .sin (4 \pi .0 - \frac{\pi }{3}) > 0 \ \ \\ a < 0 \ (Vi \ x > 0) \hspace{2,2cm} \end{matrix}\right.\)
KL: Vật có li độ x = 1,5 cm, đang chuyển động chậm dần (a.v < 0) theo chiều dương (v > 0).
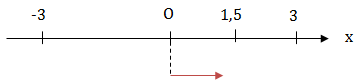
Tại \(t = 0,5 \Rightarrow \left\{\begin{matrix} x = 1,5\ cm\\ v > 0 \ \ \ \ \ \ \ \ \\ a < 0 \ \ \ \ \ \ \ \ \end{matrix}\right.\)
KL: Trạng thái tại t = 0,5s và tại t = 0 hoàn toàn giống nhau.
VD2: Cho dao động \(x = -cos (2 \pi t - \frac{\pi }{3}) \ (dm)\)
a. Xác đinh A, \(\omega\), \(\varphi\), T, \(\ell\)?
b. Xác định trạng thái dao động của vật tại cách tời điểm t1 = 0; t2 = 0,5s và t3 = 1,5s?
Giải:
Từ \(x = -cos (2 \pi t - \frac{\pi }{3}) \ (dm)\)
\(x = -10.cos (2 \pi t - \frac{\pi }{3}) \ (cm)\)
\(x = 10.cos (2 \pi t - \frac{\pi }{3} + \pi)\)
\(\Rightarrow x = 10.cos (2 \pi t + \frac{2 \pi }{3})\ (cm)\)
a.
\(A = 10(cm); \ \omega = 2\pi (\frac{rad}{s});\ \varphi = \frac{2\pi}{3}\)
\(T = \frac{2\pi}{\omega } = \frac{2\pi}{2\pi} = 1(s), \ell = 2A = 20(cm)\)
b.
Từ \(x = 10.cos (2 \pi t + \frac{2 \pi }{3})\ (cm)\)
\(\rightarrow \left\{\begin{matrix} v = -20 \pi .sin (2\pi t + \frac{2\pi}{3})\\ a = -\omega ^2.x \hspace{2,2cm} \end{matrix}\right.\)
+ Tại \(t_1 = 0: \left\{\begin{matrix} x = 10.cos(2\pi .0 + \frac{2\pi}{3}) = -5cm\\ v = -20 \pi .sin (2\pi .0 + \frac{2\pi}{3}) < 0 \ \ \ \\ a > 0 \ (Vi \ x < 0) \hspace{2,4cm} \end{matrix}\right.\)
KL: Vật có li độ -5 cm, chuyển động chậm dần (v.a < 0), theo chiều âm (v > 0)
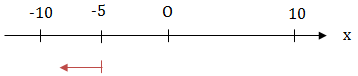
+ Tại: \(t_2 = 0,5s: \left\{\begin{matrix} x = 10.cos(2\pi .0,5 + \frac{2\pi}{3}) = 5cm\\ v = -20 \pi .sin (2\pi .0,5 + \frac{2\pi}{3}) > 0 \\ a < 0 \ (Vi \ x > 0) \hspace{2,4cm} \end{matrix}\right.\)
KL: Vật có li độ 5cm, chuyển động chậm dần (v.a < 0), theo chiều dương (v > 0)
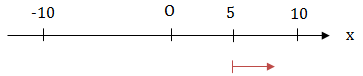
+ Tại t3 = 1,5s
⇒ Trạng thái dao động được lặp lại














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



