GIỚI THIỆU BÀI HỌC
Năng lượng điều hòa là dạng toán quan trọng nhất trong chuyên đề Dao động cơ học. Bài học giúp các em nắm được khái niệm năng lượng, cơ năng (động năng và thế năng). Có thể tìm được giá trị của động năng, thế năng, hoặc cơ năng trong dao động điều hòa và biết được các kỹ thuật biến đổi khi giải các bài toán liên quan.
NỘI DUNG BÀI HỌC
Hôm nay chúng ta xét dạng bài tập cuối cùng của bài Dao động điều hòa. Trong 11 dạng của bài đầu tiên là 11 dạng cơ bản nhất và quan trọng nhất vì nó sẽ đi với các em đến cuối năm, có trong đề thi Đại học, thậm chí những chương sau đó như: Sóng cơ, Dòng điện xoay chiều, Dao động điện từ chúng ta sẽ liên tục gặp lại những dạng này. Vì thế 11 dạng các em đã được học rất kỹ và nên ôn đi ôn lại và luyện thêm nhiều bài tập.
Dạng 11 Năng lượng của dao động điều hòa (cũng là năng lượng cơ) lại là dạng quan trọng nhất trong những dạng chúng ta đã học.
Năng lượng là đại lượng đặc trưng cho khả năng sinh công. Vậy công là gì? Khi một lực tác dụng vào vật làm cho vật đó có khả năng chuyển hoặc biến dạng thì ta nói lực đó đã thực hiện công. Làm biến dạng nhiều hay ít, dịch chuyển xa hay gần điều đó lại do năng lượng quy định, đặc trưng cho khả năng sinh công. Trong chuyển động cơ thì năng lượng trong chuyển động cơ gọi là cơ năng gồm động năng và thế năng.
+ Động năng là năng lượng do vật chuyển động sinh ra, có nghĩa là vật đang chuyển động nó sẵn sàng thực hiện công nếu như có vật chắn nó, nó có thể làm vật dịch chuyển hoặc biến dạng.
+ Thế năng trong chương trình phổ thông chúng ta xét 2 dạng cơ bản nhất là thế năng hấp dẫn và thế năng đàn hồi. Thế năng hấp dẫn là do lực hấp dẫn sinh ra (lực hút của Trái Đất). Thế năng đàn hồi do lực đàn hồi sinh ra, lò xo khi bị nén lại hoặc giãn ra nó xu hướng thực hiện công.
Ta có: \(\left\{\begin{matrix} x = A.\cos (\omega t + \varphi ) \ \ \ \\ v = - \omega A.\sin (\omega t + \varphi ) \end{matrix}\right.\)
+ Động năng: Wđ \(= \frac{1}{2}mv^2 = \frac{1}{2}m \omega ^2 A^2.\sin ^2(\omega t + \varphi )\)
+ Thế năng: \(W_t= \frac{1}{2}m\omega ^2 x^2 = \frac{1}{2}m \omega ^2A^2.\cos ^2(\omega t + \varphi )\)
+ Cơ năng:
W = Wđ + Wt = \(= \frac{1}{2}mv^2 + \frac{1}{2}m \omega ^2 x^2\)
\(W= \frac{1}{2}m \omega ^2 A^2\) (hằng số)
W = Wđ max = \(W= \frac{1}{2}m v_{max}^{2}\) (VTCB: Wt = 0)
\(W= W_{t\ max}= \frac{1}{2}m \omega ^2 A^2\) (VT biên: Wđ = 0)
* Chú ý:
(1). Khi tính Wđ, Wt, W phải đổi đơn vị về hệ SI: \(\left\{\begin{matrix} m(kg)\ \ \\ v(\frac{m}{s}) \ \ \ \ \\ x,A (m) \end{matrix}\right.\)
(2). Wđ, Wt:
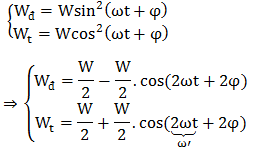
⇒ Wđ, Wt dao động TUẦN HOÀN với \(\omega ' = 2\omega\)
W là hằng số ⇒ KHÔNG dao động
* Các công thức cần nhớ
(1). W = Wđ + Wt
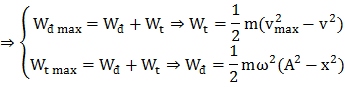
(2). Tìm x, v khi Wđ = n.Wt
+ Tìm x: Wt max = Wđ + Wt
⇒ Wt max = n.Wt + Wt = (n + 1)Wt
\(\\ \Rightarrow \frac{1}{2}m \omega ^2 A^2 = (n+1).\frac{1}{2}m \omega ^2 x^2\\ \Rightarrow A^2 = (n+1)x^2 \Rightarrow x = \pm \frac{A}{\sqrt{n+1}}\)
+ Tìm v: Wđ max = Wđ + Wt
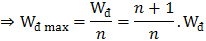
\(\Rightarrow v_{max}^{2} = \frac{n+1}{n}.v^2 \Rightarrow v = \pm v_{max}.\sqrt{\frac{n}{n+1}}\)
(3). Cho, x, v ⇒ Tìm 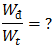
Cho x: 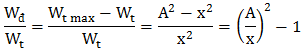
Cho v: .png)
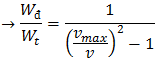
VD: Cho dao động \(x =5\cos(2\pi t - \frac{\pi}{3})\) (cm), khối lượng của vật m = 100g. Lấy \(\pi ^2 = 10\)
a. Tìm W?
b. Tìm Wđ khi x = 3 cm?
c. Tìm Wt khi v = 6\(\pi\) cm/s?
d. Tìm x, v khi Wđ = 3Wt?
e. Tìm 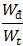 khi x = 2 cm?
khi x = 2 cm?
f. Tìm 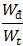 khi v = 5\(\pi\) cm/s?
khi v = 5\(\pi\) cm/s?
Giải:
m = 100g = 0,1kg
A = 5 cm = 0,05 m
a.
\(\\ W = \frac{1}{2}m\omega ^2A^2 = \frac{1}{2}.0,1.(2\pi)^2.0,05^2\\ \rightarrow W = 0,005 \ J\)
b.
Wđ \(= \frac{1}{2}m \omega ^2 A^2 - \frac{1}{2}m \omega ^2x^2\)
\(\\ = \frac{1}{2}m \omega ^2 (A^2 - x^2)\\ = \frac{1}{2}.0,1.(2\pi)^2.(0,05^2 - 0,03^2)\\ = 0,032\ J\)
c.
\(W_t= \frac{1}{2}m v_{max}^{2} - \frac{1}{2}m v^2\)
\(\\ = \frac{1}{2}m (v_{max}^{2} - v^2)\\ = \frac{1}{2}.0,1.\left [ (10 \pi)^2 - (6\pi)^2 \right ].(10^{-2})^2\\ =0,032\ J\)
d. Wđ = 3Wt
• Wt max = 3Wt + Wt = 4Wt
\(\rightarrow A^2 = 4x^2 \Rightarrow x = \pm \frac{A}{2} = \pm 2,5\ cm\)
• 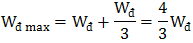
\(\\ \rightarrow \frac{1}{2}mv_{max}^{2} = \frac{4}{3}.\frac{1}{2}mv^2 \Rightarrow v = \pm v_{max}\frac{\sqrt{3}}{2} \\ \Rightarrow v = \pm 5 \pi \sqrt{3}(\frac{cm}{s})\)
e.
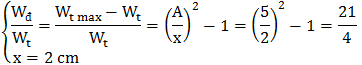
f.
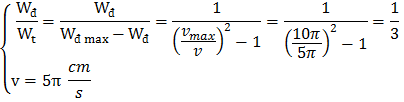














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



