Dạng 3: Bài toán va chạm

Bài giảng Bài toán va chạm nhằm giúp học sinh hiểu được khái niệm va chạm, phân biệt được từng loại va chạm và đặc điểm của chúng. Qua đó, nắm được các kiến thức cơ bản áp dụng giải các bài toán va chạm từ đơn giản đến phức tạp. Từ đó rút ra kinh nghiệm, kỹ năng giải quyết các bài toán va chạm một cách ngắn gọn và đúng nhất.

Chúng ta xét qua dạng 3: Bài toán va chạm. Ở lớp 10, chúng ta đã học về va chạm và hôm nay chúng ta sẽ tìm hiểu thêm một số dạng của bài toán va chạm có thể gặp trong các đề thi.

* Va chạm mềm (Va chạm tuyệt đối không đàn hồi)
* Trước va chạm:
+ Vật m₁ chuyển động với vận tốc \(\overrightarrow{v_1}\).
+ Vật m₂ chuyển động với vận tốc \(\overrightarrow{v_2}\).
⇒ Động lượng: \(\overrightarrow{P_t} = m_1 \overrightarrow{v_1} + m_2 \overrightarrow{v_2}\)
* Sau va chạm: hai vật dính vào nhau và cùng chuyển động với vận tốc \(\overrightarrow{v}\).
⇒ Động lượng: \(\overrightarrow{P_s} = (m_1 + m_2).\overrightarrow{v}\)
ĐLBT động lượng: \(\overrightarrow{P_s} = \overrightarrow{P_t}\)
\(\Rightarrow (m_1 + m_2)\overrightarrow{v} = m_1 \overrightarrow{v_1} + m_2 \overrightarrow{v_2}\)
Nếu \(\overrightarrow{v_1}\), \(\overrightarrow{v_2}\) cùng phương thì:
\(\Rightarrow (m_1 + m_2)v = m_1 v_1 + m_2 v_2\)
* Trong va chạm mềm không có định luật bảo toàn năng lượng (vì có nội năng sinh ra)
\(Q = \frac{1}{2} m_1 v_{1}^{2} + \frac{1}{2} m_2 v_{2}^{2} - \frac{1}{2} (m_1 + m_2)v^2\)

* Va chạm tuyệt đối đàn hồi
* Trước va chạm:
+ Vật m₁ chuyển động với vận tốc \(\overrightarrow{v_1}\).
+ Vật m₂ chuyển động với vận tốc \(\overrightarrow{v_2}\).
⇒ Động lượng: \(\overrightarrow{P_t} = m_1 \overrightarrow{v_1} + m_2 \overrightarrow{v_2}\)
* Sau va chạm: 
+ Vật m₁ chuyển động với vận tốc \(\overrightarrow{v'_1}\).
+ Vật m₂ chuyển động với vận tốc \(\overrightarrow{v'_2}\).
⇒ Động lượng: \(\overrightarrow{P_s} = m_1 \overrightarrow{v'_1} + m_2 \overrightarrow{v'_2}\)
ĐLBT động lượng: \(\overrightarrow{P_s} = \overrightarrow{P_t}\)
\(\Rightarrow m_1\overrightarrow{v'_1} + m_2\overrightarrow{v'_2} = m_1\overrightarrow{v_1} + m_2\overrightarrow{v_2}\)
Nếu \(\overrightarrow{v_1}\), \(\overrightarrow{v_2}\) cùng phương thì:
\(m_1v'_1 + m_2v'_2 = m_1v_1 + m_2v_2 \ (1)\)
ĐLBT năng lượng:
\(\frac{1}{2}m_1{v'_1}^2 + \frac{1}{2} m_2{v'_2}^2 = \frac{1}{2} m_1{v_1}^2 + \frac{1}{2} m_2{v_2}^2 \ (2)\)
Từ (1) và (2) ⇒ Kết quả

VD1: Một con lắc lò xo có độ cứng 100 N/m, vật nặng m₁ = 900 g đang nằm cân bằng trên mặt phẳng ngang. Viên dạn có khối lượng m₂ = 100 g bay với vận tốc 2 m/s theo phương trục lò xo đến va chạm mềm với m₁. Sau va chạm 2 vật cùng dao động điều hòa với biên độ A. Tìm A?
Giải:
k = 100 N/m
m₁ = 900 g, v₁ = 0
m₂ = 100 g, v₂ = 2 m/s
Theo ĐLBT động lượng: \(m_2\overrightarrow{v_2} = (m_1 + m_2) \overrightarrow{v}\)
\(\Rightarrow v = \frac{m_2v_2}{m_1+ m_2} = \frac{100.2}{900+100} = 0,2\ m/s = 20\ cm/s\)
\(\Rightarrow v_{max} = v = 20\ cm/s\)
\(\cdot \ A = \frac{v_{max}}{\omega }\)
\(\cdot \ \omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{k}{m_1 + m_2}} = \sqrt{\frac{100}{0,9+0,1}} = 10\ rad/s\)
\(\Rightarrow A = \frac{v_{max}}{\omega } = \frac{20}{10}=2\ (cm)\)

VD2: Vật có khối lượng m rơi từ độ cao h lên một đĩa cân gắn vào một lò xo có độ cứng k, vật và đĩa cân dính vào nhau dao động điều hòa. Bỏ qua khối lượng đĩa  cân, gia tốc trọng trường g, bỏ qua mọi lực cản. Tìm biểu thức biên độ A?
Giải:

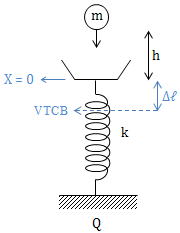
• Vận tốc của vật m khi vừa chạm đĩa cân:
\(v = \sqrt{2gh}\)
\(\Rightarrow \overrightarrow{P_t} = m \overrightarrow{v}\)
\(\overrightarrow{P_s} = \overrightarrow{P_t} = m \overrightarrow{v}\)
Tại vị trí: \(\left\{\begin{matrix} |x| = \Delta \ell \ \ \\ v = \sqrt{2gh} \end{matrix}\right.\)
\(\omega = \sqrt{\frac{k}{m}}\)
\(\Rightarrow A = \sqrt{x^2 + \frac{v^2}{\omega ^2}} = \sqrt{{\Delta \ell }^2 + \frac{2gh}{k}.m}\)