GIỚI THIỆU BÀI HỌC
Video bài giảng Những điểm đặc biệt nằm trên đường trung trực của hai nguồn cùng pha trình bày lại kiến thức theo từng phần sau: kiến thức chung, phân dạng kiến thức bài tập, đề trắc nghiệm tổng hợp. Mời các em học sinh cùng tham khảo học tập và ôn luyện hiệu quả
NỘI DUNG BÀI HỌC
* Xét 2 nguồn \(u_A=u_B=a.cos(\omega -\varphi )\)
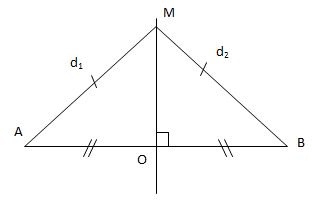
d1=d2=d
Ta có:
\(u_M=2.a.cos[\frac{\pi}{\lambda }(d_2-d_1)].cos[\omega t+\varphi -\frac{\pi }{\lambda }(d_1+d_2)]\)
Độ lệch pha của sóng tại M so với A
\(\Delta \varphi _{AM}=\left | \omega t+\varphi -(\omega+\varphi -\frac{\pi }{\lambda })(d_1+d_2) \right |\)
\(\Delta \varphi _{AM}=\frac{\pi }{\lambda }(d_1+d_2)=\frac{2\pi.d}{\lambda }\)
uM cùng pha \(u_A\Rightarrow \Delta \varphi _{AM}=k2\pi\)
\(\Rightarrow \frac{2\pi d}{\lambda }=k2\pi\Rightarrow d=k\lambda , k\in Z\)
uM ngược pha \(u_A\Rightarrow \Delta \varphi _{AM}=(2k+1)\pi\)
\(\Rightarrow \frac{2\pi d}{\lambda }=(2k+1)\pi\Rightarrow d=(2k+1)\frac{\lambda}{2} , k\in Z\)
uM vuông pha \(u_A\Rightarrow \Delta \varphi _{AM}=(2k+1)\frac{\pi}{2}\)
\(\Rightarrow \frac{2\pi d}{\lambda }=(2k+1)\frac{\pi}{2} \Rightarrow d=(2k+1)\frac{\pi}{4} , k\in Z\)
* Xét 2 điểm M, N thuộc đường trung trực AB:














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



