Dạng 2: Phương trình sóng

Mục tiêu của bài Phương trình sóng là giúp các em học sinh nắm được các kiến thức về các đặc trưng của một phương trình sóng và tổng quát về hiện tượng truyền sóng trên sợi dây .

* Xét sóng truyền từ nguồn O với phương trình \(u_O=a.cos(\omega t+\varphi )\) dọc them phương Ox. Trên phương Ox xét điểm M các O một đoạn x.

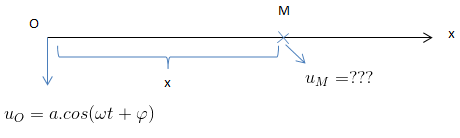
Thời gian sóng truyền từ O đến M: \(t_0=\frac{x}{v}\)
Sóng tại M vào thời điểm t trùng với sóng tại O vào thời điểm (t - t₀).
\(\Rightarrow u_M(t)=u_0(t-t_0)=a.cos[\omega (t-t_0)+\varphi ]\)
\(\Rightarrow u_M=a.cos(\omega t+\varphi -\frac{2\pi}{T }.\frac{x}{v})\)
Vậy \(u_M=a.cos(\omega t+\varphi -\frac{2\pi{x}}{\lambda })\)
* Độ lệch pha: \(\Delta \varphi =\frac{2\pi{x}}{\lambda }\)
* Chú ý: 
1.  Xét sóng cơ truyền theo phương Ox

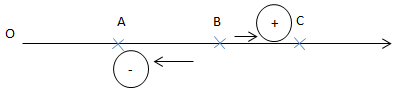
Nếu \(u_B=a.cos(\omega t+\varphi _B)\)
Thì \(\left\{\begin{matrix} u_A=a.cos(\omega t+\varphi _B+\frac{2\pi.AB}{\lambda })\\ \\ u_B=a.cos(\omega t+\varphi _B-\frac{2\pi.AB}{\lambda }) \end{matrix}\right.\)
ĐK: \(t\geq \frac{BC}{v}\)
2. Hình dạng sóng

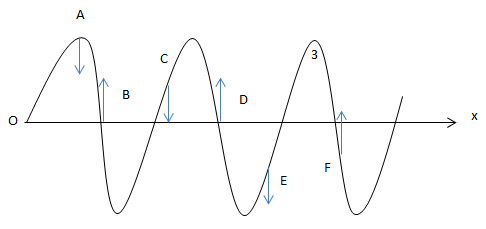
VD1: Một sợi dây đàn hồi rất dài có đầu O dao động với phương trình \(u_O=3cos(4\pit)(mm)\) cho tốc độ truyền sóng bằng 40 cm/s.
a. Viết phương trình sóng tại M trên dây cách O một đoạn 50 cm.
b. Tìm \(u_M\) tại các thời điểm \(t_1=1s, t_2=2s\)
Giải
a.
\(u_M=3.cos(4\pi t-\frac{2\pi.OM}{\lambda }) (mm)\)
\(OM=x= 50cm\)
\(T=\frac{2\pi}{\omega }=\frac{2\pi}{4 \pi}=0,5s\)
\(\Rightarrow \lambda =v.T= 40.0,5=20 cm\)
\(\Rightarrow \frac{2\pi. OM}{\lambda }=\frac{2\pi.50}{20}=5\pi\)
Vậy \(u_M=3.cos(4\pi t-5\pi) \ (mm)\)
b.
Tại t₁ = 1s
Ta có 
\(t_{OM}=\frac{OM}{v}=\frac{50}{40}=1,25s\)
\(t_1=1s<t_{OM}\Rightarrow u_{M_1}=O\)
Tại \(t_2=2s>t_{OM}\Rightarrow u_{M_1}=3cos(4 \pi.t_2-5\pi)\)
\(\Rightarrow u_{M2}=3cos(4\pi .2 - 5 \pi)=-3(mm)\)
VD2: Một sóng cơ truyền theo phương Ox với phương trình \(u=5.cos(5\pi t+\frac{\pi x}{2}-\frac{\pi}{3})(mm)\). Trong đó x(m); t(s). Tìm tốc độ truyền sóng v?
Giải
\(u=5.cos(5\pi t+\frac{\pi x}{2}-\frac{\pi}{3})(mm)\)
\(\Leftrightarrow u=5.cos(5\pi t+\frac{\pi }{3}-\frac{\pi x}{2})(mm)\)
\(u=a.cos(\omega t+\varphi -\frac{2\pi x}{\lambda })\)
\(\Rightarrow \left\{\begin{matrix} \omega t=5 \pi.t\\ \\ \frac{2 \pi.x}{\lambda }=\frac{\pi .x}{2} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \omega =5\pi \Rightarrow T=\frac{2\pi}{\omega }\ = \frac{2}{5}s \\ \lambda =4 (m) \end{matrix}\right.\)
\(\Rightarrow v=\frac{\lambda }{T}=\frac{4}{\frac{2}{5}}=10 (m/s)\)
Nhớ: 
\(=\frac{\omega }{\frac{2\pi}{\lambda }}=\omega .\frac{\lambda }{2\pi}= \frac{\lambda }{T}=v\)
Áp dụng: \(v=\frac{5\pi}{\frac{\pi}{2}}=10(m/s)\)