Dạng 9: Trong một chu kì tìm thời gian để đại lượng Vật lý P thoả điều kiện cho trước

Qua bài học này, học sinh nắm được công thức dạng tổng quát của đại lượng vật lý P, ngoài ra xác định được thời gian vật thỏa một điều kiện cho trước.

Chúng ta tiếp tục tìm hiểu dạng 9 của bài toán dao động điều hòa, trong một chu kỳ hoặc trong nửa chu kỳ (ở đây được cho thời gian cụ thể) tìm thời gian để đại lượng vật lý P thỏa điều kiện cho trước nào đó, đại lượng vật lí P ở đây có thể là li độ, vận tốc, gia tốc, lực kéo về...

Tổng quát: \(P = P_0.cos(\omega t + \varphi )\)
Trong đó:
· P: li độ ⇒ \(\left\{\begin{matrix} P_0 = A\\ P = x \ \\ T = \frac{2 \pi}{\omega } \end{matrix}\right.\)
· P: vận tốc ⇒ \(\left\{\begin{matrix} P_0 = \omega A = v_{max}\\ P = v \hspace{1,8cm}\\ T = \frac{2 \pi}{\omega } \hspace{1,6cm}\end{matrix}\right.\)
· P: gia tốc ⇒ \(\left\{\begin{matrix} P_0 = a_{max} = \omega ^2A \\ P_0 = a \hspace{1,8cm}\\ T = \frac{2 \pi}{\omega } \hspace{1,6cm}\end{matrix}\right.\)
· P: lực kéo về ⇒ \(\left\{\begin{matrix} P_0 = F_{KV_{max}} = m \omega ^2A \\ P = F_{KV} \hspace{2,2cm}\\ T = \frac{2 \pi}{\omega } \hspace{2,5cm} \end{matrix}\right.\)
Nhận xét: Các đại lượng x, v, a, F_KV dao động điều hòa cùng tần số ⇒ Cùng T.
VD: Trong 1T, tìm thời gian để độ lớn của P không vượt quá \(\frac{P_0}{n}\).
\(\Rightarrow \left\{\begin{matrix} Trong\ 1T \Rightarrow \Delta t =\ ?\\ |P| \leq \frac{P_0}{n} \hspace{2cm} \end{matrix}\right.\)

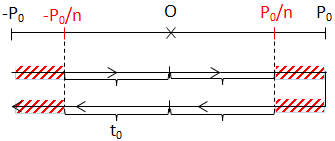
Δt = 4.t₀
• Trong \(\frac{1}{2}\)T, tìm thời gian để độ lớn P không nhỏ hơn \(\frac{P_0}{n}\).
\(\Rightarrow \left\{\begin{matrix} Trong\ \frac{1}{2}T \Rightarrow \Delta t =\ ?\\ \\|P| \geq \frac{P_0}{n} \hspace{2cm} \end{matrix}\right.\)

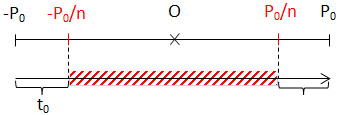
⇒ Δt = 2.t₀

VD1: Cho dao động \(x = 10 cos (8 \pi t - \frac{\pi}{8})\)(cm).
a. Trong \(\frac{1}{2}\) chu kỳ, tìm thời gian để độ lớn li độ không nhỏ hơn \(5\sqrt{3}\) cm?
b. Trong 1 chu kỳ, tìm thời gian để vận tốc của vật không lớn hơn 40\(\pi\) cm/s?
Giải:
\(T = \frac{2\pi}{\omega } = \frac{1}{4}s\)
a.
\(\left\{\begin{matrix} Trong\ \frac{1}{2}T \Rightarrow \Delta t = \ ?\\ |x| \geq 5\sqrt{3}\ (cm) = \frac{A\sqrt{3}}2{} \end{matrix}\right.\)

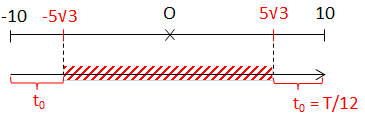
\(\Rightarrow \Delta t = 2.t_0 = 2.\frac{T}{12} = \frac{T}{6}\)
\(\Rightarrow \Delta t = \frac{1}{24}s\)
b.
\(\left\{\begin{matrix} Trong\ 1T \Rightarrow \Delta t = \ ?\\ v \leq 40\pi \left (\frac{cm}{s} \right ) = \frac{v_{max}}{2} \end{matrix}\right.\)

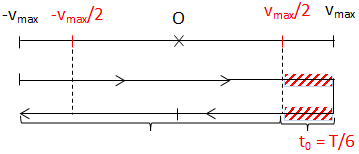
\(\Rightarrow \Delta t = T - 2.\frac{T}{6} = \frac{2T}{3} = \frac{1}{6}s\)

VD2: Một vật có khối lượng 500g dao động với phương trình \(x = 5cos(10t - \frac{\pi}{2})\) (cm). Trong 1 chu kỳ, tìm thời gian để độ lớn lực kéo về không được vượt quá 1N?
Giải:
\(T = \frac{2\pi}{\omega } = \frac{\pi}{5}(s)\)
\(F_{KV_{max}} = ma_{max} = m\omega ^2A\) (Đơn vị: m (kg); A (m))
\(F_{KV_{max}} = 0,5.10^2.5.10^{-2} = 2,5N\)
\(\Rightarrow \left\{\begin{matrix} Trong\ 1T \Rightarrow \Delta t = \ ? \hspace{1,3cm}\\ |F_{KV}| \leq 1N; F_{KV_{max}} = 2,5N \end{matrix}\right.\)

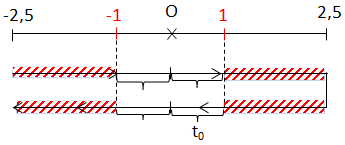
Với \(t_0 = \frac{T}{2\pi}.sin^{-1}\left ( \frac{1}{2,5} \right )\)
\(\Rightarrow \Delta t = 4.\frac{T}{2\pi}.sin^{-1}\left ( \frac{1}{2,5} \right ) \approx 0,165s\)