Bài 2: Con lắc lò xo

Bài giảng giúp học sinh nắm được các kiến thức trọng tâm về con lắc lò xo:

• Cấu tạo của con lắc xò xo
• Khảo sát chuyển động của con lắc lò xo nằm ngang, thẳng đứng và nằm nghiêng.
• Khái niệm, biểu thức lực đàn hồi
• Biết thêm công thức tính dao động điều hòa

I. Cấu tạo
Gồm:
- 1 lò xo nhẹ, độ cứng k.
- Quả cầu khối lượng m.

II. Khảo sát chuyển động của con lắc lò xo
1. Con lắc lò xo nằm ngang

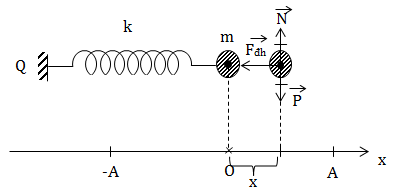
Theo đinh luật II Niuton: \(\sum \overrightarrow{F} = m\overrightarrow{a}\)
Hay: \(\overrightarrow{P} + \overrightarrow{N} + \overrightarrow{F_{dh}} = m \overrightarrow{a} \ (\ast )\)
Chiếu (*) lên Ox: F_dh = ma
Với \(\left\{\begin{matrix} F_{dh} = -k.x\\ a = x'' \ \ \ \ \ \ \end{matrix}\right. \ \ \Rightarrow -k.x = m.x'' \Leftrightarrow x'' = -\frac{k}{m}.x\)
Đặt \(\omega ^2 = \frac{k}{m} \Rightarrow x'' = -\omega ^2.x \ (**)\)
Nghiệm (**) có dạng: \(x = A\cos (\omega t + \varphi )\)
Vậy: Dao động của con lắc lò xo là dao động điều hòa với chu kỳ \(T = \frac{2\pi}{\omega } = 2\pi \sqrt{\frac{m}{k}}\)
2. Con lắc lò xo treo thẳng đứng

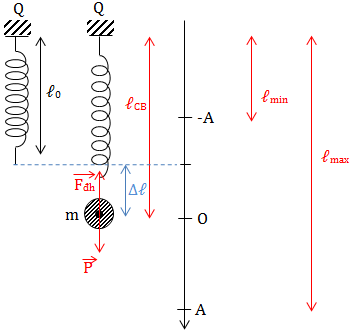
* Tại VTCB: \(\overrightarrow{F_{dh}} + \overrightarrow{P} = \overrightarrow{O} \Rightarrow F_{dh} = P\)
\(\Rightarrow k.\Delta \ell = mg \Rightarrow \left\{\begin{matrix} \Delta \ell = \frac{mg}{k} \ \ \ \ \ \ \\ \omega ^2=\frac{k}{m} = \frac{g}{\Delta \ell } \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} T = \frac{2\pi }{\omega } = 2 \pi \sqrt{\frac{k}{m}} = 2 \pi \sqrt{\frac{\Delta \ell }{g}} \\ f = \frac{1}{T} = \frac{\omega }{2 \pi} = \frac{1}{2 \pi}\sqrt{\frac{k}{m}} = \frac{1}{2 \pi}\sqrt{\frac{g}{\Delta \ell}} \end{matrix}\right.\)
* Chú ý: Đối với con lắc lò xo thì chu kỳ (T) tần số (f) không phụ thuộc g và \(\Delta \ell\)

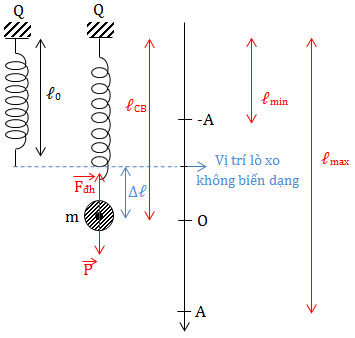
\(\cdot \ \ell _{CB} = \ell _{o} + \Delta \ell\)
\(\left.\begin{matrix} \cdot \ \ell _{max} = \ell _{CB} + A \\ \cdot \ \ell _{min} = \ell _{CB} - A \\ \end{matrix}\right\} \Rightarrow \left\{\begin{matrix} \ell _{CB} = \frac{\ell _{max} + \ell _{min}}{2}\\ A = \frac{\ell _{max} - \ell _{min}}{2} \ \ \ \end{matrix}\right.\)
* Lực đàn hồi: Là lực sinh ra khi lò xo bị biến dạng, \(\overrightarrow{F_{dh}}\) luôn hướng về vị trí lò xo không biến dạng, có độ lớn tỉ lệ với độ biến dạng của lò xo.
* Biểu thức: \(F_{dh} = kX\)
Với k: độ cứng (N/m); x: độ biến dạng (m)
\(F_{dh \ max} = kX_{max} = k(\Delta \ell + A)\)
\(F_{dh\ min} = \left\{\begin{matrix} 0\ neu \ A \geq \Delta \ell\ \hspace{1,5cm}\\ k(\Delta \ell - A) \ neu \ A < \Delta \ell \end{matrix}\right.\)
3. Con lắc lò xo nằm nghiêng

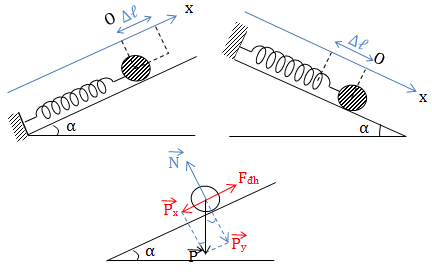
Tại VTCB: \(\overrightarrow{P} + \overrightarrow{N} + \overrightarrow{F_{dh}} = \overrightarrow{O}\)
\(\Rightarrow P_X = F_{dh}\) với \(\left\{\begin{matrix} P_x = m.g\sin \alpha \\ F_{dh} = k.\Delta \ell \end{matrix}\right.\)
\(\Rightarrow k.\Delta \ell = m.g\sin \alpha\)
\(\Rightarrow \omega ^2 = \frac{k}{m}=\frac{g.\sin \alpha }{\Delta \ell}\)
\(\cdot \ T = \frac{2 \pi}{\omega } = 2 \pi \sqrt{\frac{k}{m}} = 2 \pi \sqrt{\frac{\Delta \ell }{g\sin \alpha }}\)
\(\cdot \ f = \frac{\omega }{2 \pi } = \frac{1}{2 \pi} \sqrt{\frac{k}{m}} = \frac{1}{2 \pi} \sqrt{\frac{g\sin \alpha }{\Delta \ell}}\)
Nhận xét:
(1) Đối với con lắc lò xo nằm ngang:
\(\overrightarrow{F_{dh}} = \overrightarrow{F_{hp}}\) (VTCB trùng với vị trí lò xo không biến dạng)
(2) Đối với con lắc lò xo thẳng đứng, nằm nghiêng:
\(\overrightarrow{F_{dh}} \neq \overrightarrow{F_{hp}}\) (VTCB khác với vị trí lò xo không biến dạng)
\(\Rightarrow \overrightarrow{F_{hp}} = \overrightarrow{F_{dh}} + \overrightarrow{P}\) (con lắc lò xo thẳng đứng)