Dạng 1: Giao thoa với ánh sáng đơn sắc

Qua bài này, các em sẽ được làm quen với dạng bài đầu tiên của hiện tượng giao thoa ánh sáng cùng với các bài tập liên quan theo nhiều cấp độ từ dễ đến khó…, các em cần phải nắm được : 

• Mô tả được thí nghiệm Y-âng về giao thoa ánh sáng.

• Viết được các công thức cho vị trí của các vân sáng, tối và cho khoảng vân i.

• Giải được bài toán về giao thoa với ánh sáng đơn sắc.

Nguồn S phát ra ánh sáng đơn sắc có bước sóng \(\lambda\)

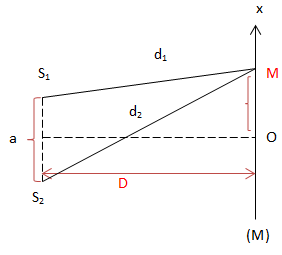
* Tại M là vân sáng (cực đại giao thoa)
Ta có: \(d_2-d_1=\frac{a.x}{D}\)
\(d_2-d_1=\frac{a.x_s}{D}=k.\lambda \Rightarrow x_s=k.\frac{\lambda .D}{a}; k\in Z\)
Với \(k = 0\Rightarrow x_{S_0}=0\) vân sáng trung tâm
\(k = \pm 1\Rightarrow x_{S_1}=\pm \frac{\lambda .D}{a}\) vân sáng bậc 1
\(k = \pm 2\Rightarrow x_{S_2}=\pm 2. \frac{\lambda .D}{a}\) vân sáng bậc 2
* Tìm M là vân tối (cực tiểu giao thoa)
\(d_2-d_1=\frac{a.x_t}{D}=(k'+\frac{1}{2})\lambda \Rightarrow x_t=(k'+\frac{1}{2}).\frac{\lambda .D}{a}, k'\in Z\)
Với \(\Bigg \lbrack\begin{matrix} k'=0\Rightarrow x_{t_1}=\frac{1}{2}.\frac{\lambda .D}{a}\\ \\ k'=-1\Rightarrow x_{t_1}=-\frac{1}{2}.\frac{\lambda .D}{a} \end{matrix}\) vân tối thứ 1
\(\Bigg \lbrack\begin{matrix} k'=1\Rightarrow x_{t_2}=\frac{3}{2}.\frac{\lambda .D}{a}\\ \\ k'=-2\Rightarrow x_{t_2}=-\frac{3}{2}.\frac{\lambda .D}{a} \end{matrix}\) vân tối thứ 2
VD1: Trong thí nghiệm Yâng về giao thoa ánh sáng, lai khe S₁S₂ cách nhau 1mm, khoảng cách từ mặt phẳng chứa 2 khe đến màn quan sát là 2m. Nguồn S phát ra ánh sáng đơn sắc có bước sóng \(0,5\mu m\).
a. Tìm khoảng cách giữa 2 vân sáng bậc 3?
b. Tìm khoảng cách giữa 2 vân tối thứ 5?
c. Xác định cường độ sáng tại M có \(x_M=8,5mm\)
d. Cho L = 2, 35cm. Tìm số vân sáng và vân tối quan sát được?
Giải
a = 1mm; D = 2m; \(\lambda =0,5\mu m\)
\(\Rightarrow i=\frac{\lambda .D}{a}=\frac{0,5.2}{1}=1(mm)\)
a. 
\(\Delta x_{S_3}=2.3i=2.3.1=6(mm)\)
b.
\(\Delta x_{t5}=(2.5-1).i=(2.5-1).1=9 (mm)\)
c.
\(\frac{x_M}{i}=\frac{8,5}{1}=8,5\Rightarrow\) M thuộc vân tối thứ 9
d.
L= 2,35 cm = 23,5 (mm)
\(\frac{L}{i}=\frac{23,5}{1}=23,5\)
⇒ Trên L có \(\left\{\begin{matrix} 23 \ VS\\ 24 \ VT \end{matrix}\right.\)
VD2: Trong thí nghiệm Yâng, nguồn S phát ra bước xạ đơn sắc \(\lambda\). Khoảng cách từ màn đến mặt phẳng chứa 2 khe S₁S₂ không đổi khoảng cách giữa 2 khe S₁S₂ thay đổi được (S₁S₂ luôn cách đều S). Ban đầu tại M là vân sáng bậc 4, nếu tăng hoặc giảm khoảng cách 2 khe S₁S₂ một lượng \(\Delta a\) thì tại M là vân sáng bậc 3k và vân sáng bậc k. Nếu tăng khoảng cách 2 khe một lượng 2.\(\Delta a\) thì tại M là vân gì? bậc mấy?
Giải
\(x_M=4.i=4.\frac{\lambda .D}{a}\)
\(x_M=3k.\frac{\lambda .D}{a+\Delta a}\)
\(x_M=k.\frac{\lambda .D}{a-\Delta a}\)
\(\Rightarrow \frac{3}{a+\Delta a}=\frac{1}{a-\Delta a}\Rightarrow \Delta a= \frac{a}{2} \ (*)\)
\(\Rightarrow x_M=4.i=n\frac{\lambda .D}{a+2\Delta a} \ \ (**)\)
Từ (*) và (**) \(\Rightarrow 4.\frac{\lambda .D}{a}=n.\frac{\lambda .D}{a+2\frac{a}{2}}=n.\frac{\lambda .D}{2a}\)
\(\Rightarrow \frac{n}{2}=4\Rightarrow n=8\)
Vậy lúc này tại M là vân sáng bằng 8.