Bài 4: Mẫu nguyên tử bo

Mẫu nguyên tử Bo là sự phối hợp giữa mẫu nguyên tử Rutherford cùng với 2 tiên đề Bo về các trạng thái dừng, các quỹ đạo dừng và về sự hấp thụ và bức xạ năng lượng của nguyên tử. Thông qua những nội dung được đề cập tới trong bài học, mời các bạn cùng nghiên cứu Bài 4: Mẫu nguyên tử bo

I. Mô hình hành tinh nguyên tử
+ Năm 1911, Rutherford mạnh dạn đề sướng mẫu hành tinh nguyên tử.
+ Năm 1913, Niels Bosh (Bo) → Mẫu nguyên tử Bo.
II. Hai tiên đề Bo
1. Tiên đề về trạng thái dừng
- Nguyên tử chỉ tồn tại trong những trạng thái có NL hoàn toàn xác định, gọi là trạng thái dừng. Ở trạng thái dừng, nguyên tử không bức xạ.
+ Trong các trạng thái dừng, electron chuyển động trên những quỹ đạo hoàn toàn xác định gọi là quỹ đạo dừng.

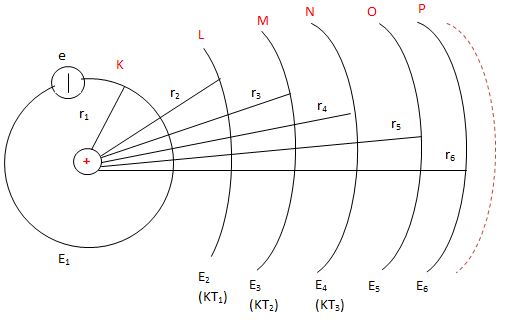
Với \(E_n=-\frac{13,6}{n^2} \ (eV)\)
\(\Rightarrow E_1=-13,6(eV);E_2=\frac{E_1}{4};E_3=\frac{E_1}{9};...\)
\(r_n=n^2.r_0;r_0=5,3.10^{-11}(m)\) bk Bo
\(\Rightarrow r_1=r_0;r_2=4.r_0=9r_0,...\)
2. Tiên đề về bức xạ và hấp thụ của nguyên tử.
- Khi nguyên tử ở trạng thái dừng có mức NL \(E_n\), nhảy về trạng thái dừng có mức NL, \(E_m\) thấp hơn thì phát ra 1 photon có NL \(E_{nm}=E_m-E_n\) và ngược lại.

III. Quang phổ vạch của Hidrô

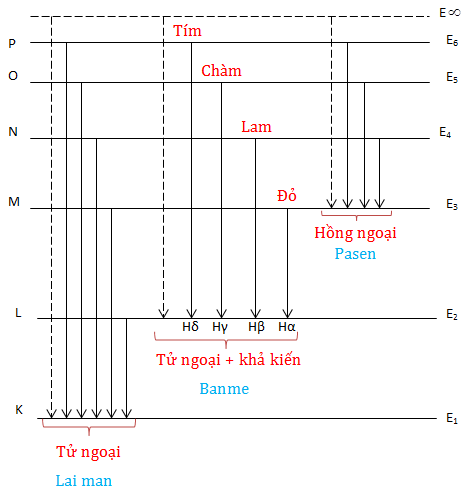
* Các dạng bài tập

1. Áp dụng công thức:
\(\left\{\begin{matrix} E_n=-\frac{13,6}{n^2}(eV)\\ r_n=n^2.r_0,r_0=5,3.10^{-11} \end{matrix}\right.\)
\(\varepsilon _{nm}=h.f{nm}=E_n-E_m=E_n-E_p+E_p-E_m=hf_{np}+hf_{pm}\)
\(\Rightarrow f_{nm}=f_{np}+f_{pm}=f_{np}-f_{mp}\)
\(\Rightarrow \frac{1}{ _{nm}}=\frac{1}{\lambda_{np}}+ \frac{1}{\lambda_{pm}}=\frac{1}{\lambda_{np}}-\frac{1}{\lambda_{mp}}\)
VD1: \(\frac{1}{\lambda _{32}}=\frac{1}{\lambda _{31}}-\frac{1}{\lambda _{21}}\)
2. Vận tốc của electron trên quỹ đạo dừng n:
Ta có: F_đt = F_ht \(\Rightarrow k.\frac{e^2}{r^2_m}=m.\frac{v^2}{r_m}\)
\(\Rightarrow v^2=\frac{k}{m}.\frac{e^2}{r_m}=\frac{k}{m}.\frac{e^2}{n^2.r_0}\)
\(\Rightarrow v=\frac{\left | e \right |}{n}.\sqrt{\frac{k}{m.r_0}}\)
VD1: Khi nguyên tử hidro ở trạng thái n thì năng lượng và bán kính được xác định \(E_n=-\frac{13,6}{n^2}\) và \(r_n=n^2.r_0\), với \(n_0=5,3.10^{-11}(m)\). Khi bán kính của electron bằng 2,12.10^-10 (m) thì năng lượng của nó bằng bao nhiêu?
Giải
Ta có
 \(r_n=n^2.r_0\)
\(\Rightarrow 2,12.10^{-10}=n^2.5,3.10^{-11}\Rightarrow n^2=4\)
⇒ Năng lượng \(E_n=\frac{13,6}{n^2}=-\frac{13,6}{4}=-3,4 \ eV\)
VD2: Khi nguyên tử hidro chuyển từ trạng thái E₄ về E₂ thì phát ra photon có bước sóng \(\lambda _{42}\). Khi nguyên tử hidro chuyển từ trạng thái E₅ về E3 thì phát ra photon có bước sóng \(\lambda _{53}\). Tìm \(\frac{\lambda _{53}}{\lambda _{42}}\) = ?
Giải
Ta có
\(\left.\begin{matrix} \varepsilon _{42}=\frac{hc}{\lambda _{42}}=E_4-E_2\\ \varepsilon _{53}=\frac{hc}{\lambda _{53}}=E_5-E_3 \end{matrix}\right\} \ \frac{\varepsilon _{42}}{\varepsilon _{53}}=\frac{\lambda _{53}} {\lambda _{42}}=\frac{E_4-E_2}{E_5-E_3}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{13,6}{4^2} -(-\frac{13,6}{2^2})}{-\frac{13,6}{5^2}-(-\frac{13,6}{3^2})}\)
\(\Rightarrow \frac{\lambda _{53}}{\lambda _{42}}=\frac{-\frac{1}{4^2}+\frac{1}{2^2}} {-\frac{1}{5^2}+\frac{1}{3^2}}=\frac{675}{256}\)