Dạng 7: Tìm quãng đường S vật đi được trong thời gian ∆t

Bài học giúp học sinh ứng dụng sơ đồ thời gian xác định quãng đường S vật đi được trong thời gian Δt, qua đó thực hành giải các bài toán liên quan.

Bữa trước các em đã được học dạng 6 là Ứng dụng của sơ đồ thời gian. Ứng dụng đầu tiên là chúng ta tìm thời điểm vật qua vị trí x0 nào đó lần thứ n. Và hôm nay chúng ta qua tiếp dạng 7 Tìm quãng đường S vật đi được trong thời gian ∆t cũng là ứng dụng của sơ đồ thời gian.

NHỚ:
+ Trong thời gian 1T ⇒ S = 4A
+ Trong thời gian \(\frac{T}{2}\) ⇒ S = 2A
+ Trong thời gian \(\frac{T}{4}\) ⇒ S = A
(Chỉ đúng khi vật đi từ x = 0 hoặc \(x = \pm A\))
* Xét \(\frac{\Delta t}{T} = a\)
\(\\ \cdot \ \bigg \lbrack \begin{matrix} a = k \ \ \ \ \ \\ a = k + \frac{1}{2} \end{matrix} \ \ \ (K \in Z) \Rightarrow S = a \times 4A \\ \cdot \ \bigg \lbrack \begin{matrix} a \neq k \ \ \ \ \ \\ a \neq k + \frac{1}{2} \end{matrix} \ \ \ (K \in Z) \Rightarrow a = k + \frac{p}{q} \ (p < q) \\ \Rightarrow \Delta t = a.T = \left (k + \frac{p}{q} \right ).T = \underbrace{kT}_{\substack{k.4A}} + \underbrace{\frac{p}{q}.T}_{\substack{S_0}}\\ \Rightarrow S = k.4A + S_0\)
S₀ được tìm dựa vào sơ đồ
+ Với ∆t = t₂ – t₁
+ Trạng thái dao động tại t₁ và t₂
+ Vẽ sơ đồ ⇒ Tìm S₀ ⇒ Kết quả

VD1: Cho dao động \(x = 4.cos(2 \pi t + \frac{\pi}{3})\) (cm).
a. Tìm quãng đường vật đi trong các khoảng thời gian ∆t₁ = 2s; ∆t₂ = 3,5s; ∆t₃ = s; từ t = 0?
b. Tìm quãng đường vật đi từ t₁ = s đến t₂ = s?
Giải:
\(T = \frac{2 \pi}{\omega } = \frac{2 \pi}{2 \pi} = 1s\)
a.
\(\\ \cdot \ \frac{\Delta t_1}{T} = \frac{2}{1} = 2 \Rightarrow S = 2.4.4 = 32\ cm\\ \cdot \ \frac{\Delta t_2}{T} = \frac{3,5}{1} = 3,35 \Rightarrow S = 3,5.4.4 = 56\ cm\\ \cdot \ \frac{\Delta t_3}{T} = \frac{\frac{25}{6}}{1} = \frac{25}{6} = 4 + \frac{1}{6} \Rightarrow \Delta t_3 = 4T + \frac{T}{6}\)
\(\\ \cdot \ t_1 = 0 \Rightarrow x_1 = 2\ cm; \ v_1 < 0\\ \cdot \ t_2 = \Delta t_3 = \frac{25}{6}s \Rightarrow x_2 = -2\ cm;\ v_2 < 0\)

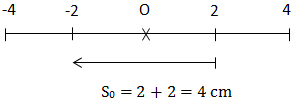
⇒ S = 4. 4. 4 + 4 = 68 cm
b.
\(\frac{\Delta t}{T} = \frac{t_2 - t_1}{T} = \frac{\frac{19}{3}-\frac{13}{12}}{1} = \frac{63}{12} = \frac{21}{4} = 5 + \frac{1}{4} \Rightarrow \Delta t = 5T + \frac{T}{4}\)
\(\\ \cdot \ t_1 = \frac{13}{12}s \Rightarrow x_1 = 0;\ v_1 < 0\\ \cdot \ t_2 = \frac{19}{3}s \Rightarrow x_2 = -4 \ cm;\ v_2 = 0\)

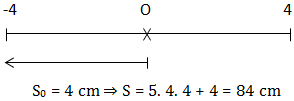
VD2: Cho dao động \(x = 6cos(5\pi t - \frac{ \pi }{4})\) (cm). Tìm quãng đường vật đi từ thời điểm \(t_1 = \frac{7}{60}s\) đến t₂ = 6,73s?
Giải:
\(T = \frac{2 \pi}{\omega } = \frac{2 \pi}{5 \pi} = 0,4s\)
\(\\ \cdot \ \frac{\Delta t}{T} = \frac{t_2 - t_1}{T} = \frac{6,73 - \frac{7}{60}}{0,4} = \frac{248}{15}\\ \Rightarrow \frac{\Delta t}{T} = 16 + \frac{8}{15} \Rightarrow \Delta t = 16.T + \frac{8T}{15}\)
Tại \(t_1 = \frac{7}{60}s \Rightarrow \left\{\begin{matrix} x_1 = 6cos(5 \pi . \frac{7}{60} - \frac{\pi}{4}) = 3\\ v_1 < 0 \hspace{3,4cm} \end{matrix}\right.\)
Tại \(t_2 = 6,73s \Rightarrow \left\{\begin{matrix} x_2 = 6cos(5 \pi .6,73 - \frac{\pi}{4}) = -1,85\\ v_2 > 0 \hspace{4,7cm} \end{matrix}\right.\)

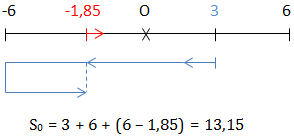
⇒ S = 16. 4. 6 + 13,15 = 397,5 cm