GIỚI THIỆU BÀI HỌC
Hôm nay chúng ta tìm hiểu về dạng 3 của bài toán Công suất, đó là Thay đổi một trong các đại lượng để Pmax , đây cũng là một trong những dạng bài quan trọng của chương Điện xoay chiều. Sau khi học xong bài này các em sẽ thấy có nhiều vấn đề liên quan đến cộng hưởng điện.
NỘI DUNG BÀI HỌC
* Thay đổi L, C, \(\omega\) để Pmax
Ta có: \(P = RI^2 = R. \frac{U^2}{R^2 + (Z_L - Z_C)^2}\)
Khi L, C, \(\omega\) thay đổi ⇒ \((Z_L - Z_C)^2\) thay đổi
\(\Rightarrow P_{max} \Leftrightarrow Z_L - Z_C = 0 \Leftrightarrow Z_L = Z_C\): Xảy ra cộng hưởng điện
Lúc này: \(\left\{\begin{matrix} P_{max} = UI_{max} = RI_{max}^{2} = \frac{U^2}{R}\\ (\cos \varphi )_{max} = 1 \hspace{2,6cm} \end{matrix}\right.\)
* Thay đổi R để Pmax
Ta có: \(P = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2} = \frac{U^2}{\frac{R^2 + (Z_L - Z_C)^2}{R}}\)
\(\Leftrightarrow P = \frac{U^2}{R + \frac{(Z_L - Z_C)^2}{R}}\)
Do U không đổi \(\Rightarrow P_{max} \Leftrightarrow \left [ R + \frac{(Z_L - Z_C)^2}{R} \right ]_{min}\)
Mà: \(R + \frac{(Z_L - Z_C)^2}{R} \geq 2|Z_L - Z_C|\)
Dấu "=" xảy ra khi \(R = \frac{(Z_L - Z_C)^2}{R} \Rightarrow R = |Z_L - Z_C|\)
Vậy thay đổi R để Pmax thì:
\(\left\{\begin{matrix} R = |Z_L - Z_C| \hspace{3,8cm} \\ P_{max} = \frac{U^2}{2R} = \frac{U^2}{R}\cos ^2 \varphi \Rightarrow \cos ^2 \varphi = \frac{1}{2}\\ \cos \varphi = \frac{1}{\sqrt{2}} = 0,707 \hspace{3cm} \end{matrix}\right.\)
* Cuộn dây có điện trở r

\(\\ \cdot \ Z_d = \sqrt{r^2 + Z_{L}^{2}} \Rightarrow U_d= \sqrt{U_{r}^{2} + U_{L}^{2}} \\ \cdot \tan \varphi _d = \frac{Z_L}{r}'\ \cos \varphi _d = \frac{r}{Z_d} = \frac{r}{\sqrt{r^2 + Z_{L}^{2}}} \\ \cdot P_{cd} = rI^2 = r\frac{U^2}{(R + r)^2 + (Z_L - Z_C)^2}\)
* Thay đổi R để (Pmạch)max
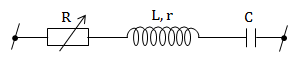
Ta có \(P_{mach} = R_b.\frac{U^2}{R_{b}^{2} + (Z_L - Z_C)^2},\ R_b = R + r\)
⇒ (Pmạch)max khi \(\left\{\begin{matrix} R_b= |Z_L - Z_C| \ \ \\ (P_{mach})_{max} = \frac{U^2}{2R_b} \end{matrix}\right.\)
Nếu \(r \geq |Z_L - Z_C| \Rightarrow R_b = r\) (Lúc này R = 0)
* Thay đổi R để (PR)max
Ta có: \(P_R = R.I^2 = R.\frac{U^2}{(R+r)^2 + (Z_L - Z_C)^2} = \frac{U^2}{R + \frac{r^2 + (Z_L - Z_C)^2}{R}+2r}\)
Do U không đổi \(\Rightarrow (P_R)_{max} \Leftrightarrow \left [ R + \frac{r^2 + (Z_L - Z_C)^2}{R} \right ]_{min}\)
Mà: \(R + \frac{r^2 + (Z_L - Z_C)^2}{R}\geq 2.\sqrt{r^2 + (Z_L - Z_C)^2}\)
Dấu "=" xảy ra khi: \(R = \sqrt{r^2 + (Z_L - Z_C)^2}\)
Lúc này: \((P_R)_{max} = \frac{U^2}{2(R+r)}\)
VD1: Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số góc thay đổi được vào hai đầu mạch RLC ghép nối tiếp khi f = f1 thì Pmax = 200 W. Khi f = f2 thì điện áp hai đầu đoạn mạch lệch pha nhau \(\frac{\pi }{6}\) so với điện áp hai đầu tụ C. Tìm P lúc này?
Giải:
\(f = f_1 \Rightarrow P_{max} = 200 = \frac{U^2}{R}\) (CHĐ)
f = f2 ⇒ u lệch pha \(\frac{\pi }{6}\) so với uC
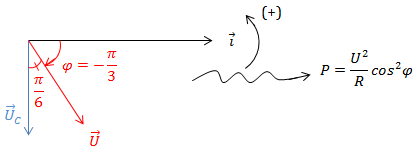
\(\Rightarrow P = P_{max}.\cos ^2 \varphi\)
Vậy: \(P = 200.\cos ^2 \left ( -\frac{\pi }{3} \right ) = 50\ V\)
VD2: Đặ điện áp \(u = 200\sqrt{2}\cos (100 \pi t - \frac{\pi }{4})\) (V) vào hai đầu đoạn mạch RLC ghép nối tiếp gồm \(R = 60 \ \Omega,\ L = \frac{6}{5 \pi } \ H,\ C = \frac{10^{-4}}{2 \pi }F\) thì công suất tiêu thụ của mạch là P1. Thay R bằng R' thì công suất tiêu thụ mạch cực đại và bằng P2. Tìm \(\frac{P_2}{P_1}\)?
Giải:
\(Z_L = L\omega = 120\ \Omega ; \ Z_C = \frac{1}{C\omega } = 200 \ \Omega\)
Ta có: \(P_1 = R.\frac{U^2}{R^2 + (Z_L - Z_C)^2} = 60.\frac{200^2}{60^2 + (120 - 200)^2} = 240\ (W)\)
Thay R = R' thì \(P_{max} = \left\{\begin{matrix} R' = |Z_L - Z_C| = 80\ \Omega \\ P_{max} = P_2 = \frac{U^2}{2R'} \hspace{1,3cm} \end{matrix}\right.\)
\(\Rightarrow P_2 = \frac{200^2}{2.80} = \frac{200^2}{160} = 250\ (W)\)
\(\Rightarrow \frac{P_2}{P_1} = \frac{250}{240} = \frac{25}{24}\)
VD3: Cho mạch điện 
\(u_{AB} = 100\sqrt{2}\cos 100 \pi t \ (V);\ r = 30\ \Omega ;\ L = 318\ mH;\ C = \frac{10^{-3}}{6 \pi }F\). Khi R = R1 thì (PR)max. Khi R = R2 thì (PAB)max. Tìm tỉ số R1 và R2?
Giải:
\(\\Z_L = L\omega = 318.10^{-3}.100\pi = 100\ \Omega \\ Z_C = \frac{1}{C\omega } = \frac{1}{\frac{10^{-3}}{6\pi }.100 \pi } = 60\ \Omega \\ \cdot \ R = R_1 \Rightarrow (P_R)_{max} \Rightarrow R_1 = \sqrt{r^2 + (Z_L - Z_C)^2}\\ \Rightarrow R_1 = \sqrt{30^2 + (100-60)^2} = 50\ \Omega \\ \cdot \ R = R_2 \Rightarrow (P_{AB})_{max} \Rightarrow R_2 + r = |Z_L - Z_C| \\ \Rightarrow R_2 + 30 = |100-60| = 40 \Rightarrow R_2 = 10\ \Omega\)
Vậy: \(\frac{R_1}{R_2} = \frac{50}{10}= 5\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



