Bài 1: Mạch dao động

Hôm nay chúng ta bắt đầu học chuyên đề 4: Dao động và sóng điện từ. Ở chuyên đề này có liên quan và gần giống với ba chuyên đề trước chúng ta đã học: vừa có dao động, vừa có sóng là sự lan truyền dao động và của điện. Bài học đầu tiên chúng ta cùng nghiên cứu là Mạch dao động, các kiến thức liên quan đến Mạch dao động, Dao động điện từ tự do và Năng lượng điện từ.

Ở chương này, phần bài tập có cách biến đổi hoàn toàn tương tự như chuyên đề 1, cách biến đổi về nguyên tắc làm không khác nhau nhiều, chỉ khác các kí hiệu. Nếu ở chuyên đề 1 các em đã nắm vững thì ở chuyên đề này các em không có gì phải lo lắng. Các em chỉ cần thuộc một số công thức cơ bản nhất, từ đó với kiến thức Toán học nền tảng chúng ta biến đổi các công thức này.

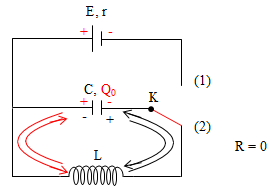
* Nguyên tắc hoạt động mạch LC: dựa vào hiện tượng TỰ CẢM.
Ta có: \(u = \frac{q}{C};\ u = e-i.R = e\)
\(e = -\phi ' = -(Li)' = -Li' = -Lq''\)
\(\Rightarrow \frac{q}{C} = -Lq'' \Leftrightarrow q'' = -\frac{1}{LC}q\)
Đặt \(\omega ^2 = \frac{1}{LC} \Rightarrow q'' = -\omega ^2.q \ (*)\)
Nghiệm của phương trình (*) có dạng \(q = Q_0\cos (\omega t + \varphi )\)
Vậy điện tích của mạch LC lý tưởng dao động điều hòa với tần số góc \(\omega = \frac{1}{\sqrt{LC}}\)
→ Chu kỳ: \(T = \frac{2 \pi }{\omega } = 2 \pi .\sqrt{LC}\)
→ Tần số: \(f = \frac{1}{T} = \frac{1}{2\pi .\sqrt{LC}}\)

* Phương trình điện áp: \(u = \frac{q}{C} = \frac{Q_0}{C}.\cos (\omega t + \varphi )\)
\(\Rightarrow u = U_0.\cos (\omega t + \varphi ),\ \ \ U_0 = \frac{Q_0}{C}\)

* Phương trình cường độ dòng điện: \(i = q' = -\omega Q_0.\sin (\omega t + \varphi )\)
\(\Rightarrow i = I_0.\cos (\omega t + \varphi + \frac{\pi}{2}),\ \ \ I_0 = \omega Q_0\)
\(T = \frac{2\pi }{\omega } = 2\pi \sqrt{LC} = 2\pi \frac{Q_0}{I_0}\)

* Mối liên hệ về pha: Trong mạch LC lý tưởng, điện tích q và điện áp u luôn dao động cùng pha và cùng trễ pha \(\frac{\pi }{2}\) so với i.

* Công thức độc lập thời gian:
\(\cdot \ q\perp i \Rightarrow \left ( \frac{q}{Q_0} \right )^2 + \left ( \frac{i}{I_0} \right )^2 = 1 \Leftrightarrow Q_{0}^{2} = q^2 + \left ( \frac{i}{\omega } \right )^2\)
\(\cdot \ u \perp i \Rightarrow \left ( \frac{u}{U_0} \right )^2 + \left ( \frac{i}{I_0} \right )^2 = 1 \Leftrightarrow u = \pm U_0\sqrt{1-\left ( \frac{i}{I_0} \right )^2}\)

* Dao động điện có sự tương tự với dao động cơ
Khi thay q ⇔ x; Q₀ ⇔ A; i ⇔ v,...

* Năng lượng mạch LC
+ Năng lượng điện trường: \(W_C = \frac{1}{2}Cu^2 = \frac{1}{2}CU_{0}^{2}.\cos ^2(\omega t + \varphi )\)
+ Năng lượng từ trường: \(W_L = \frac{1}{2}Li^2 = \frac{1}{2}LI_{0}^{2}.\sin ^2(\omega t + \varphi )\)
+ Năng lượng điện từ: \(W = W_C + W_L = \frac{1}{2}Cu^2 + \frac{1}{2}Li^2 = \frac{Q_{0}^{2}}{2C}\) (hằng số)
\(W = W_{C\ max}\ (W_L = 0)\)
\(W = W_{L\ max}\ (W_C = 0)\)

VD: Cho mạch LC lý tưởng gồm L = 4 mH; C = 9 nF; U₀ = 12 V
a) Tìm \(\omega\), T, f, I₀, Q₀, W?
b) Viết biểu thức q biết tại t = 0, \(q = \frac{Q_0}{2}\) và đang tăng? Suy ra biểu thức u và i?
c) Tìm \(\frac{W_C}{W_L}\) khi i = 3 mA và khi u = 4 V?
d) Trong 1 chu kỳ, tìm thời gian để độ lớn cường độ dòng điện i không vượt quá \(9\sqrt{3}\) mA?
Giải:
L = 4 mH = 4.10^-3 H
C = 9 nF = 9.10^-9 F
U₀ = 12 V
a)
\(\cdot \ \omega = \frac{1}{\sqrt{LC}} = \frac{1}{\sqrt{4.10^{-3}.9.10^{-9}}} = \frac{10^6}{6}\ (rad/s)\)
\(\cdot \ T = \frac{2\pi }{\omega } = \frac{2\pi }{\frac{10^6}{6}} = 12\pi .10^{-6} \ (s)\)
\(\cdot \ f = \frac{1}{T} = \frac{1}{12\pi .10^{-6}} = \frac{10^6}{12\pi }\ (Hz)\)
\(\cdot \ I_0 = \omega Q_0\)
\(\cdot \ Q_0 = CU_0 = 9.10^{-9}.12 = 108.10^{-9} \ (C)\)
\(I_0 = \omega Q_0 = \frac{10^6}{6}.108.10^{-9} = 18.10^{-3}\ (A) = 18\ (mA)\)
\(W = \frac{1}{2}CU_{0}^{2} = \frac{1}{2}.9.10^{-9}.12^2 = 648.10^{-9}\ (J)\)
b) \(q = Q_0 \cos (\omega t + \varphi )\)
\(t = 0: \left\{\begin{matrix} q = \frac{Q_0}{2} \Rightarrow \frac{Q_0}{2} = Q_0 \cos \varphi \Rightarrow \cos \varphi = \frac{1}{2} \Rightarrow \varphi = \pm \frac{\pi}{3}\\ dang\ tang \Rightarrow \varphi =\frac{\pi }{3} \hspace{5,2cm} \end{matrix}\right.\)
Vậy \(q = 108.10^{-9}.\cos (\frac{10^6}{6} t - \frac{\pi }{3}) \ (C)\)
\(\Rightarrow \left\{\begin{matrix} u = 12\cos \left ( \frac{10^6}{6}t - \frac{\pi }{3} \right )\ (V) \hspace{1cm}\\ i = 18\cos \left ( \frac{10^6}{6}t - \frac{\pi }{3} + \frac{\pi }{2} \right )\ (mA) \end{matrix}\right.\)
c) 
\(\cdot \ \left\{\begin{matrix} \frac{W_C}{W_L} = \ ? \ \ \ \\ i = 3\ mA \end{matrix}\right.\)
\(\frac{W_C}{W_L} =\frac{W-W_L}{W_L} = \frac{W}{W_L} - 1 = \frac{\frac{1}{2}LI_{0}^{2}}{\frac{1}{2}Li^2} - 1 = \left ( \frac{I_0}{i} \right )^2 - 1 = 35\)
\(\cdot \ \left\{\begin{matrix} \frac{W_C}{W_L} = \ ? \ \ \\ u = 4\ V \end{matrix}\right.\)
\(\Rightarrow \frac{W_C}{W_L} = \frac{W_C}{W-W_C} = \frac{\frac{1}{2}Cu^2}{\frac{1}{2}CU_{0}^{2}-u^2} = \frac{u^2}{U_{0}^{2}-u^2} = \frac{1}{8}\)
d) \(\left\{\begin{matrix} Trong \ 1T \hspace{4cm}\\ |i| \leq 9\sqrt{3}\ mA = \frac{I_0\sqrt{3}}{2} \Rightarrow \Delta t= \ ? \end{matrix}\right.\)

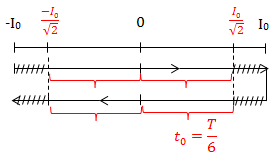
\(\Rightarrow \Delta t = 4t_0 = 4\frac{T}{6} = \frac{2}{3}.12\pi .10^{-6} = 8\pi .10^{-6}\ (s)\)