Bài 9: Bài toán viết phương trình mặt phẳng

I. Lý thuyết
Dạng \(Ax+By+Cz+D=0 \ \(A^2+B^2+C^2\neq 0)\)
\(\overrightarrow{n}=(A;B;C)\) là VTPT

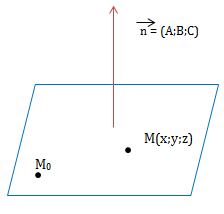
\(\left\{\begin{matrix} 1 \ VTPT \ \vec{n}=(A;B;C)\\ M_0(x_0;y_0;z_0) \end{matrix}\right.\)
\(Pt \ A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)
Chú ý:
1) Mp đi qua A(a;0;0), B(0;b;0), C(0;0;c) có pt \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
2) Một số cách xác định VTPT
\(\left.\begin{matrix} \vec{n}\perp \overrightarrow{u_1}\\ \vec{n}\perp \overrightarrow{u_2} \end{matrix}\right\}\) chọn \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\)
\(\overrightarrow{u_1}=(a_1;b_1;c_1)\)
\(\overrightarrow{u_2}=(a_2;b_2;c_2)\)
\(\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ] = \left ( \begin{vmatrix} b_1 \ \ c_1\\ b_2 \ \ c_2 \end{vmatrix}; \begin{vmatrix} c_1 \ \ a_1\\ c_2 \ \ a_2 \end{vmatrix}; \begin{vmatrix} a_1 \ \ b_1\\ a_2 \ \ b_2 \end{vmatrix}\right )\)

\(= (b_1.c_2-b_2c_1;c_1.a_2-c_2a_1;a_1.b_2-a_2b_1)\)
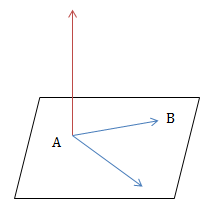
Mp(ABC) có 1 VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\)



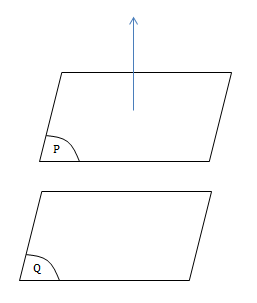
3) (P) // (Q)
\(\overrightarrow{n}_P\) là 1VTPT của (P)
\(\overrightarrow{n}_P\) là 1VTPT của (Q)


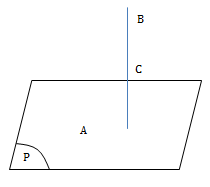
4)
\(\bigg \lbrack \begin{matrix} AB\subset (P)\\ AB //(P) \end{matrix}\Rightarrow \vec{n_P}\perp \overrightarrow{AB}\)
5) 
\((P)\perp (Q)\Rightarrow \overrightarrow{n}_P\perp \overrightarrow{n}_Q\)
II. Bài tập
VD1: Cho A(-1;2;3), B(2;-4;3), C(4;5;6). Viết phương trình mp (P) đi qua A và vuông góc BC.
Giải
(P) đi qua A(-1;2;3) và vuông góc BC nên nhận \(\overrightarrow{BC}=(2;9;3)\) làm 1 VTPT
pt (P): \(2(x+1) +9(y-2)+3(z-3)=0\)
\(\Leftrightarrow 2x+9y+3z-25=0\)

VD2: Viết phương trình mặt phẳng (ABC) biết A(1;2;3), B(2;-1;1), C(3;0;-2)
Giải
\(\overrightarrow{AB}=(1;-3;-2)\)
\(\overrightarrow{AC}=(2;-2;-5)\)
\(\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]= \left ( \begin{vmatrix} -3 \ -2\\ -2 \ -5 \end{vmatrix}; \begin{vmatrix} -2 \ \ \ \ 1\\ -5 \ -2 \end{vmatrix}; \begin{vmatrix} 1 \ -3\\ 2 \ -2 \end{vmatrix} \right ) =(11;1;4)\)
(ABC) đi qua A(1;2;3) và nhận \(\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]=(11;1;4)\) làm VTPT
pt (ABC) \(11(x-1)+1(y-2)+4(z-3)=0\)
\(\Leftrightarrow 11x+y+4z-25=0\)
VD3: Viết phương trình mặt phẳng trung trực của đoạn AB, A(1;2;4), B(-3;0;2)
Giải
Gọi I là trung điểm AB
I(-1;1;3)
Mặt phẳng trung trực của đoạn AB đi qua I(-1;1;3) và nhận \(\overrightarrow{AB}=(-4;-2-2)\) làm VTPT nên có phương trình 
\(-4(x+1)-2(y-1)-2(z-3)=0\)
\(\Leftrightarrow 2(x+1)+y-1+z-3=0\)
\(\Leftrightarrow 2x+y+z-2=0\)
VD4: Trong không gian Oxyz cho A(-1;2;3), (Q); y - z -1 = 0. Viết phương trình \((\alpha )\) đi qua A và song song (Q)
Giải
\((\alpha )\) // (Q): y - z - 1 = 0 nên \((\alpha )\) nhận
\(\overrightarrow{n}_Q=(0;1;-1)\) là 1 VTPT
pt \((\alpha )\)  \(0(x+1)+1(y-2)-1(z-3)=0\)
\(y-z+1=0(t/m \ \(\alpha ) // (Q))\)
VD5: Trong không gian Oxyz cho A(-1;2;3); (P) x+y+1=0, (Q) 2x -y+z-14=0
Viết phương trình \((\alpha)\) đi qua A và đồng thời vuông góc với (P) (Q)
Giải
Gọi \(\vec{n}\) là 1 VTPT của \((\alpha)\) ta có
\((\alpha)\) \(\perp\) (P) nên \(\overrightarrow{n}\) \(\perp\) \(\overrightarrow{n}_P\) = (1;1;0)
\((\alpha)\) \(\perp\) (Q) nên \(\overrightarrow{n}\) \(\perp\) \(\overrightarrow{n}_Q\) = (2;-1;1)
Chọn \(\vec{n}=\left [ \overrightarrow{n}_P;\overrightarrow{n}_Q \right ] =\left ( \begin{vmatrix} 1 \ \ 0\\ -1 \ \ 1 \end{vmatrix}; \begin{vmatrix} 0 \ \ 1\\ 1 \ \ 2 \end{vmatrix}; \begin{vmatrix} 1 \ \ 1\\ 2 \ \ -1 \end{vmatrix} \right )=(1;-1;-3)\)
pt \((\alpha)\) 
\(1(x+1)-(y-2)-3(z-3)=0\)
\(x-y-3z+12=0\)
VD6: Trong không gian Oxyz, cho A(-1;2;3). (P) x + y +1 = 0 (Q) 2x - y + z -14 = 0. Viết phương trình mặt phẳng A và giao tuyến của (P) và (Q)
Giải
\((\alpha)\) đi qua giao tuyến (P), (Q) nên pt \((\alpha)\) có dạng \(m(x+y+1) + n(2x-y+z-14) = 0 \ \ (m^2+n^2\neq 0)\)
\(A(-1;2;3)\in (\alpha )\) nên
2m - 15 n = 0
Chọn m = 15, n = 2 
Ta có phương trình \((\alpha)\)
\(15(x+y+1)+2(2x-y+z-14)=0\)
\(19x+13y+2z-13=0\)