Bài 4: Ứng dụng của thể tích tính khoảng cách, chứng minh hệ thức

I. Lý thuyết
V_Kchóp = \(\frac{1}{3}\) h.S
⇒ d(đỉnh, đáy) = \(\frac{3V_{chop}}{S_{day}}\)
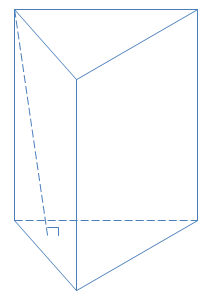
V_{lăng trụ} = h. S_đáy
\(\Rightarrow d(2 \ day) = \frac{V_{K.lang \ tru}}{S_{day}}\)
= d(đỉnh thuộc đáy này, đáy kia)


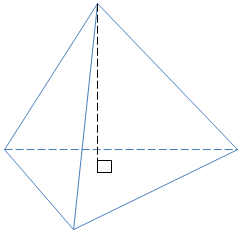
VD1 (D-2002): Cho tứ diện ABCD có \(AD\perp (ABC), AD=AC=4, AB=3, BC=5\). Tính d(A;BDC)).
Giải

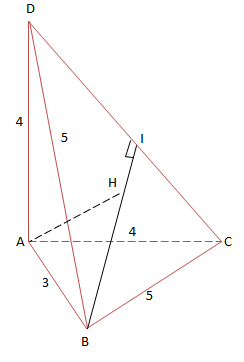
\(V_{A.BCD}=V_{D.ABC}\)
\(AB^2+AC^2=BC^2=25\)
⇒ AB \(\perp\) AC
\(S_{\Delta ABC}=\frac{1}{2}AB.AC=6\)
\(V_{A.BCD}=V_{DABC}=\frac{1}{3}.AD.S_{\Delta ABC}=\frac{1}{3}.4.6=8\)
Xét \(\Delta ABD \ \ BD^2=AB^2+AD^2=3^2+4^2=25\Rightarrow BD=5\)\(\Delta ADC \ \ DC^2=AD^2+AC^2=4^2+4^2=32\Rightarrow DC=4\sqrt{2}\)
\(BI=\sqrt{BD^2-DI^2}=\sqrt{25-(2\sqrt{2})^2}=\sqrt{17}\)
\(S_{\Delta BCD}=\frac{1}{2}.BI.DC=\frac{1}{2}.\sqrt{17}.4\sqrt{2}=2.\sqrt{34}\)
\(d(A;(DBC))=\frac{3V_{A.DBC}}{S_{\Delta BDC}}=\frac{24}{2\sqrt{34}}=\frac{ 12}{\sqrt{34}}=\frac{6\sqrt{34}}{17}\)
VD2: Cho lăng trụ ABC.A'B'C' có độ dài cạnh bên bằng 2a, đáy ABC là tam giác vuông tại A, AB = a, AC = \(a\sqrt{3}\), hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm BC. Tính d(A';(BCC'B')

Giải
\(d(A';(BCC'B'))=\frac{3V_(A'.BCC'B')}{S_{BCC'B'}}\)
Gọi H là trung điểm BC. Ta có \(A'H\perp (ABC)\)
\(AH=\frac{1}{2}BC=\frac{1}{2}.\sqrt{AB^2+AC^2}=\frac{1}{2}\sqrt{a^2+3a^2}= a\)

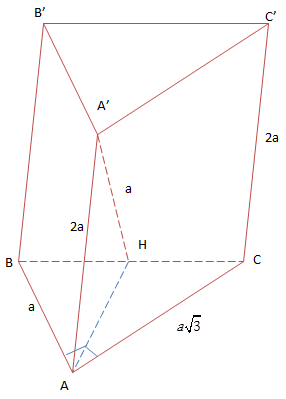
Trong \(\Delta A'HA\)
\(A'H=\sqrt{AA'^2-AH^2}=\sqrt{4a^2-a^2}=a\sqrt{3}\)
\(V_{A'ABC}=\frac{1}{3}.A'H.\frac{1}{2}AB.AC=\frac{1}{6}.a\sqrt{3}.a.a\sqrt{3}=\frac{a^3}{2}\)
\(V_{ABC.A'B'C}=A'H.\frac{1}{2}.AB.AC=\frac{3a^2}{2}\)
\(V_{A'BCC'B}=V_{ABC.A'B'C'}-V_{A'ABC}=\frac{3a^3}{2}-\frac{a^3}{2}=a^3\)
\(A'H\perp (ABC)\Rightarrow A'H\perp AB\)
\(\Rightarrow A'H\perp A'B'\)
Trong \(\Delta HA'B'\)
\(\Delta HB'^2=\sqrt{HA'^2+A'B'^2}=\sqrt{3a^2+a^2}=2a\)

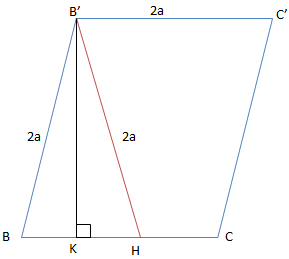
Gọi K là trung điểm BH
ta có \(B'K\perp BH(do \ B'B=B'H=2a)\)
\(B'K'=\sqrt{BB'^2-BK^2}=\sqrt{4a^2-(\frac{2a}{4})^2}=a.\frac{\sqrt{15}}{2}\)
\(S_{BCC'B'}=B'K.BC=a\frac{\sqrt{15}}{2}.2a=a^2\sqrt{15}\)
\(d(A';(BCC'B'))=\frac{3V_{A'BCC'B'}}{S_{BCC'B'}}=\frac{3a^3}{a^2\sqrt{15}}= \frac{3a}{\sqrt{15}}=\frac{a\sqrt{15}}{5}\)
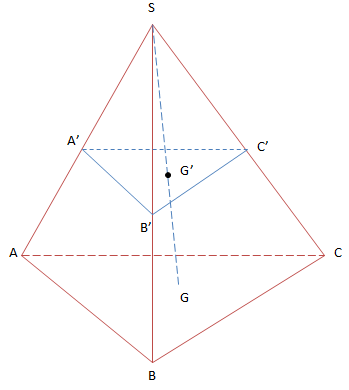
VD3: Cho hình chóp S.ABC A', B' C' lần lượt thuộc cạnh SA, SB, SC. G là trọng tâm \(\Delta\)ABC. G' là giao điểm của SG với (A'B'C'). CMR: \(\frac{SA}{SA'}+\frac{SB}{SB'}+\frac{SC}{SC'}=3\frac{SG}{SG'}\)
Giải
\(\frac{V_{SA'B'C'}}{V_{SBC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}(1)\)
\(\frac{V_{SA'B'C'}}{V_{SBC}}=\frac{V_{SG'A'B'}}{3.V_{SGAB}}+ \frac{V_{SG'A'C'}}{3.V_{SGAC}}+\frac{V_{SG'B'C'}}{3.V_{SGBC}}\)
(do dt ABC = 3dt GAB = 3dt GAC = 3dt GBC)
\(=\frac{1}{3}\frac{SG'}{SG}.\frac{SA'}{SA}.\frac{SB'}{SB}+ \frac{1}{3}\frac{SG'}{SG}.\frac{SA'}{SA}.\frac{SC'}{SC}+ \frac{1}{3}\frac{SG'}{SG}.\frac{SB'}{SB}.\frac{SC'}{SC} \ (2)\)

Từ (1) (2)
\(\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}=\frac{1}{3}\frac{SG'}{SG}.\frac{SA'}{SA}.\frac{SB'}{SB}+ \frac{1}{3}\frac{SG'}{SG}.\frac{SA'}{SA}.\frac{SC'}{SC}+ \frac{1}{3}\frac{SG'}{SG}.\frac{SB'}{SB}.\frac{SC'}{SC}\)
Nhân 2 vế với \(3.\frac{SA}{SA'}.\frac{SB}{SB'}.\frac{SC}{SC'}.\frac{SG}{SG'}\) 
ta có \(3.\frac{SG}{SG'}=\frac{SA}{SA'}+\frac{SB}{SB'}+\frac{SC}{SC'}\)