Bài 11: Bài toán khoảng cách từ điểm đến mặt phẳng

I. Lý thuyết
Cho (P) \(Ax+By+Cz+D=0 \ \ (A^2+B^2+C^2\neq 0)\)
và điểm M(x₀; y₀; z₀)
\(d(M;(P))=\frac{\left | Ax_0+Ay_0+Az_0+D \right |}{\sqrt{A^2+B^2+C^2}}\)
II. Bài tập
VD1: Cho (P) \(mx+2y+2z+3=0\) và M (1;2;3)
a) Với m = 1. Tính d(M; (P))
b) Tìm m để d(M;(P)) = 5
Giải
\(d(M;(P))=\frac{\left | m+4+6+3 \right |}{\sqrt{m^2+2^2+2^2}}= \frac{\left | m+13 \right |}{\sqrt{m^2+8}}\)
a)
\(m=1 \ \ . d(M,(P))=\frac{14}{\sqrt{9}}=\frac{14}{3}\)
b)
\(d(M;(P))=5\Leftrightarrow \frac{\left | m+13 \right |}{\sqrt{m^2+8}}=5\)
\(\Leftrightarrow \left | m+13 \right |=5.\sqrt{m^2+8}\)
\(\Leftrightarrow m^2+26m+169=25(m^2+8)\)
\(\Leftrightarrow 24m^2-26m-31=0\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} m=\frac{13-\sqrt{744}}{24}\\ \\ m=\frac{13+\sqrt{744}}{24} \end{matrix}\)
VD2: Cho 
\(\begin{matrix} (P): x+2y+2z+3=0\\ (Q):x+2y+2z-5=0 \end{matrix}\)
a) Tính d((P), (Q))
b) Viết phương trình mặt phẳng (R) song song với (P), (Q) đồng thời cách đều (P) và (Q).
Giải
a)
\(N(x_0;y_0;z_0)\in (P)\)
\(\Rightarrow x_0+2y_0+2z_0+3=0\)
\(d(N;(Q))=\frac{\left | x_0+2y_0+2z_0-5 \right |}{\sqrt{1^2+2^2+2^2}} =\frac{\left | -3-5 \right |}{3}=\frac{8}{3}\)
Nhận xét:
\(\left.\begin{matrix} (P): Ax+By+Cz+D=0\\ (Q): Ax+By+Cz+D'=0 \end{matrix}\right\}d(P;Q)=\frac{\left | D-D' \right |}{\sqrt{A^2+B^2+C^2}}\)b)
\((R) //(P)\) nên R có dạng
\(x+2y+2z+d=0 \, d\neq 3, d\neq -5\)
\(d(R;Q)=\frac{\left | d-3 \right |}{\sqrt{1^2+2^2+2^2}}=\frac{\left | d-3 \right |}{3}\)
\(d(R;Q)=\frac{\left | d+5\right |}{\sqrt{1^2+2^2+2^2}}=\frac{\left | d+5 \right |}{3}\)
\(d(R;P)=d(R;Q)\Leftrightarrow \left | d+5 \right |=\left | d-3 \right |\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} d+5=d-3\\ d+5=-d+3 \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix} 0=-8 (vo \ li)\\ d=-1 \end{matrix}\)
Vậy (R): 2x + 2y +2z - 1 = 0
VD3: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(5;1;3), B(1;6;2), C(5;0;4), D(4;0;6). Tính độ dài đường kẻ từ A của tứ diện.
Giải

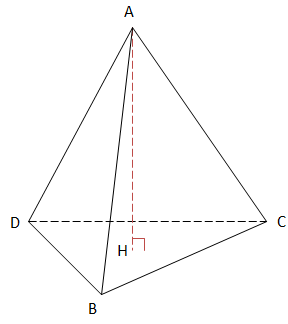
\(\overrightarrow{BC}=(4;-6;2)\)
\(\overrightarrow{BD}=(3;-6;4)\)
\(\left [ \overrightarrow{BC}; \overrightarrow{BD} \right ]= \left ( \begin{vmatrix} -6 \ 2\\ -6 \ 4 \end{vmatrix}; \begin{vmatrix} 2 \ 4\\ 4 \ 2 \end{vmatrix}; \begin{vmatrix} 4 \ -6\\ 3 \ -6 \end{vmatrix} \right )=(-12;-10;6)\)
(BCD) nhận \(\left [ \overrightarrow{BC}; \overrightarrow{BD} \right ]=(-12;-10;6)\) hay \(\vec{n}=(-6;-5;3)\) làm 1 VTPT
pt (BCD) \(-6(x-1)-5(y-6)+3(z-2)=0\)
\(\Leftrightarrow -6x-5y+3z+30=0\)
Độ dài đường cao AH là 
\(AH=d(A;(BCD))=\frac{\left | -30-5+9+30 \right |}{\sqrt{(-6)^2+(-5)^2+3^2}}= \frac{4}{\sqrt{70}}\)
VD4: Viết phương trình (P) đi qua giao tuyến của 2 mp (R) x - 3y - 2 = 0, (Q) y + 5z - 1 = 0 và có khoảng cách từ A(1;-1;0) đến (P) bằng 1.
Giải
(P) đi qua giao tuyến của (R) và (Q) nên có phương trình dạng.
\(m(x-3y-2)+n(y+5z-1)=0 \ (m^2+n^2\neq 0)\)
\(\Leftrightarrow mx+(-3m+n)y+5nz-2m-n=0\)
\(d(A;(P))=1\Leftrightarrow \frac{\left | m+3m-n-2m-n \right |}{\sqrt{m^2+(-3m+n)^2}+25n^2}=1\)
\(\Leftrightarrow \left | 2m-2n \right |=\sqrt{m^2+9m^2-6mn+n^2+25n^2}\)
\(\Leftrightarrow 4m^2+4n^2-8mn=10m^2-6mn+26n^2\)
\(\Leftrightarrow 6m^2+2mn-22n^2=0\)
\(\Leftrightarrow 3m^2+mn-11n^2=0 \ \ (1)\)
Nếu n = 0 thì m = 0 (vô lý)
Nếu \(n\neq 0\) chia 2 vế cho n², ta có
\(3\left ( \frac{m}{n} \right )^2+\frac{m}{n}-11=0\)
\(\Delta =1-4.3(-11)=1+132=133\)
\(\Bigg \lbrack \begin{matrix} \frac{m}{n}=\frac{-1-\sqrt{133}}{6}\\ \\ \frac{m}{n}=\frac{-1+\sqrt{133}}{6} \end{matrix}\)
TH1: 
\(\frac{m}{n}=\frac{-1-\sqrt{133}}{6}\), chọn \(m=-1-\sqrt{133}, n=6\)
pt (P) \((-1-\sqrt{133})x+(9+3\sqrt{133})y+30z-4+2\sqrt{133}=0\)
TH2:
\(\frac{m}{n}=\frac{-1+\sqrt{133}}{6}\), chọn \(m=-1+\sqrt{133}, n=6\)
pt (P) \((-1+\sqrt{133})x+(9-3\sqrt{133})y+30z-4-2\sqrt{133}=0\)