Bài 9: Bài toán tìm GTLN, GTNN của hàm số

1. Lý thuyết 

a) M được gọi là GTLN f(x) trên D nếu
$\left\{\begin{matrix} f(x)\leq M\\ \exists x_0, f(x_0)=M \end{matrix}\right.$
m=GTNN f(x) nếu  $\left\{\begin{matrix} m\leq f(x), \forall x\in D\\ \forall x_0\in D, f(x_0)=m \end{matrix}\right.$
 

b) Bài toán 1

Tìm GTLN, NN trên D

+ Lập BBT trên D

+ Từ BBT suy ra KL

 Bài toán 2
Tìm GTLN, NN trên [a;b]
+ Tìm nghiệm f'(x) =0 trên [a;b] giả sử x₁, x_{2
$\begin{matrix} GTLN f(x) = GTLN f(x) \\ [a;b] \ \ \ \ \ \ [a;b] \end{matrix}\left\{\begin{matrix} f(a), f(b), f(x_1)...f(x_n) \\ \end{matrix}\right.$
$\begin{matrix} GTNN f(x) = GTNN f(x) \\ [a;b] \ \ \ \ \ \ [a;b] \end{matrix}\left\{\begin{matrix} f(a), f(b), f(x_1)...f(x_n) \\ \end{matrix}\right.$}
2. Bài tập
VD1: Tìm GTLN, NN của $f(x)=x^3-3x$  trên [-2;3]
Giải
$f'(x)=3x^2-3$
$f'(x)=0\Leftrightarrow \begin{bmatrix} x=1\\ x=-1 \end{matrix}$

f(-2) = -2

f(1) = -1

f(3) = 18

f(-1) = 2
$\underset{[-2;3]}{GTLN} f(x) = 18$ khi x= 3
$\underset{[-2;3]}{GTNN} f(x) = -2 \ khi \ \bigg \lbrack\begin{matrix} x=-2\\ x=1 \end{matrix}$
 

VD2: Tìm GTNN của $f(x)=x+\frac{1}{x}$ trên $[2;+\infty )$
Giải
$f'(x)=1-\frac{1}{x^2}=\frac{x^2-1}{x^2}$
$f'(x)=0\Leftrightarrow x^2-1=0$
$\Leftrightarrow \bigg \lbrack\begin{matrix} x=1\notin [2;+\infty )\\ x=-1\notin [2;+\infty ) \end{matrix}$

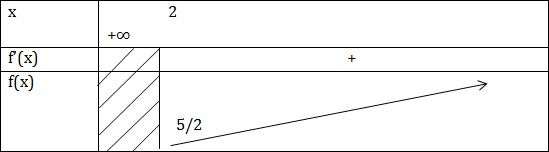
$\underset{[2;+\infty ]}{GTNN} f(x) = \frac{5}{2} \ khi \ x = 2$
VD3: Tìm GTLN của $f(x)=\sqrt{x}+\sqrt{2-x}$
TXĐ: [0;2]
$f'(x)=\frac{1}{2\sqrt{x}}-\frac{1}{2\sqrt{2-x}}$
$f'(x)=0\Leftrightarrow \sqrt{x}-\sqrt{2-x}\Leftrightarrow x=1$
$f(0)=\sqrt{2}$
$f(x)=\sqrt{2}$
$f(1)=\sqrt{2}$
$\underset{[0;2]}{GTLN}f(x)=2 \ khi \ x=1$
$\underset{[0;2]}{GTLN}f(x)=\sqrt{2} \ khi \ \left\{\begin{matrix} x=0\\ x=2 \end{matrix}\right.$
VD4: Tìm GTNN của hàm số $f(x)=sin^3x-3sin^2x$
Giải
Đặt t = sinx $t \in [-1;1]$
Bài toán trở thành tìm GTLN, GTNN của
$g(t)=t^3-3t^2$ trên [-1;1]
$g'(t)=3t^2-6t$
$g'(t)=0\Leftrightarrow 3t(t-2)=0$
$\Leftrightarrow \bigg \lbrack\begin{matrix} t=0\\ t=2\notin [-1;1] \end{matrix}$
g(0) = 0
g(-1) = -4, g(1) =-2
$\underset{[-1;1]}{GTLN}g(t)=0 \ khi \ t=0$
$\Leftrightarrow sinx=0\Leftrightarrow x=k\pi (k\in z)$
$\underset{[-1;1]}{GTNN}g(t)=-4 \ khi \ t =1$
$\Leftrightarrow sinx=-1\Leftrightarrow x=-\frac{\pi}{2}+k2\pi$
KL: GTLN f(x) = 0 khi  $x=k\pi$
GTNN f(x) = -4 khi $x=-\frac{\pi}{2}+k2\pi$
VD5: Tìm GTLN của hàm số $f(x)=\frac{x+3}{\sqrt{x^2+1}}$
Giải
$f'(x)=\frac{\sqrt{x^2+1}-\frac{2x(x+3)}{2\sqrt{x^2+1}}}{x^2+1}$
$=\frac{x^2+1-x^2-3x}{(x^2+1)\sqrt{x^2+1}}$
$=\frac{1-3x}{(x^2+1)\sqrt{x^2+1}}$
$f'(x)=0\Leftrightarrow 1-3x=0$
$\Leftrightarrow x=\frac{1}{3}$


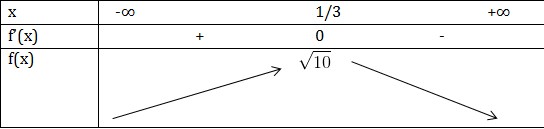
$GTLN f(x)=\sqrt{10} \ khi \ x = \frac{1}{3}$
Khai thác bt: 
$\frac{x+3}{\sqrt{x^2+1}}\leq \sqrt{10}\Rightarrow \frac{1}{\sqrt{10}}(x+3)\leq \sqrt{x^2+1}$
BT cho x + y + z = 1. Tìm $GTNN T=\sqrt{x^2+1}+\sqrt{y^2+1}+\sqrt{z^2+1}$