Bài 8: Tìm tham số để hàm số đạt cực trị thỏa mãn điều kiện cho trước

Trong bài học hôm nay chúng ta xét bài toán Tìm tham số để hàm số đạt cực trị thỏa mãn điều kiện cho trước.

VD1: Tìm m để hàm số \(f(x)=(m+2)x^3+3x^2+mx-5\)
a) Có cực trị
b) Có cực đại, cực tiểu
Giải
TXĐ: D= R
\(f'(x)=3(m+2)x^2+6x+m\)
TH 1: \(m+2=0\Leftrightarrow m=-2\)
\(f'(x)=6x-2\)
\(f'(x)=0\Leftrightarrow x=\frac{1}{3}\)

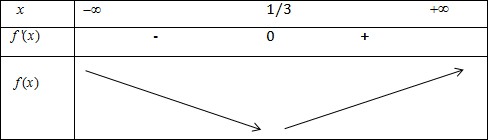
Hàm số đạt cực tiểu tại x_CT = 1/3, m = -2 (thỏa mãn)
TH2: \(m+2\neq 0\)
Hàm số có cực trị khi f'(x) = 0 có 2 nghiệm phân biệt
\(\Leftrightarrow 3(m+2)x^2+6x+m=0\)
\(\Delta '=9-3m(m+2)>0\)
\(\Leftrightarrow 3-m(m+2)>0\)
\(\Leftrightarrow -m^2-2m+3>0\)
\(\Leftrightarrow -3< m< 1\)
KL: \(-3< m< 1\)
b) Hàm số có cực đại, cực tiểu khi 
\(\left\{\begin{matrix} 3(m+2)\neq 0\\ \Delta '>0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq -2\\ -m^2-2m+3>0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq -2\\ -3<m<1 \end{matrix}\right.\)
Vậy \((-3;-2)\cup (-2;1)\)
Chú ý: f(x) = ax³+bx²+cx+d (a≠0)
Hàm số có cực đại, cực tiểu ⇔ f’(x) = 0 có 2 nghiệm phân biệt f’(x) =0 có nghiệm kép, hàm số không có cực trị.
VD2: Tìm m để hàm số \(f(x)=x^3-3x^2+3mx+3m+4\) không có cực trị
Giải
TXĐ: D = R
\(f'(x)=3x^2-6x+3m\)
Hàm số không có cực trị khi f'(x) = 0 vô nghiệm hoặc có nghiệm kép 
\(\Delta '\leq 0\Leftrightarrow 9-9m\leq 0\)
\(\Leftrightarrow 1-m\leq 0\)
\(\Leftrightarrow m\geq 1\)
Vậy \(m\geq 1\) thì hàm số không có cực trị

Chú ý:
Hàm số f(x) = ax³+bx²+cx+d (a≠0) không có cực trị khi \(\Delta _{f'(x)}\leq 0\)
VD3: Tìm m để hàm số \(f(x)=mx^4+(m^2-9)x^2+10\) có 3 cực trị
Giải
TXĐ: D = R
\(f'(x)=4mx^3+2(m^2-9)x\)
Để hàm số có 3 cực trị thì f’(x) = 0 có 3 nghiệm phân biệt
\(2x[2mx^2+m^2-9]=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow \bigg \lbrack \begin{matrix} x=0\\ 2mx^2=9-m^2 \end{matrix}\) có 2 nghiệm phân biệt khác 0
Khi \(2m(9-m^2)>0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} m<-3\\ 0<m<3 \end{matrix}\)
Vậy \(\bigg \lbrack\begin{matrix} m<-3\\ 0<m<3 \end{matrix}\)

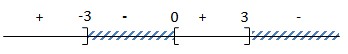
VD4: Tìm m để hàm số \(f(x)=x^3-3mx^2+(m^2-1)x+2\) đạt cực đại tại x = 2
Giải
TXĐ: D = R
\(f'(x)=3x^2-6mx+m^2-1\)
ĐK cần: Hàm số đạt cực đại tại x = 2 thì
\(f'(2)=0\Leftrightarrow 12-12m+m^2-1=0\)
\(\Leftrightarrow m^2-12m+11=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} m=1\\ m=11 \end{matrix}\)
ĐK đủ: m=1
\(f'(x)=3x^2-6x\)
\(f'(x)=0\Leftrightarrow 3x(x-2)=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=0\\ x=2 \end{matrix}\)
\(f''(x)=6x-6\)
\(f''(0)=-6<0\Rightarrow x_{CD}=0\)
\(f''(2)=6>0\Rightarrow x_{CT}=2\)
m = 1 không thỏa mãn
m = 11
\(f'(x)=3x^2-66x+120\)
\(f''(x)=6x-66\)
\(f''(2)=12-66=-54<0\)
\(\Rightarrow x_{CD}=2\)
Vậy m =11 (thỏa mãn)
VD5: Tìm m để đường thẳng đi qua các cực trị của đồ tị hàm số \(f(x)=x^3-3x^2+3mx+3m+4\) đi qua A(1;4)
Giải
TXĐ: D = R
\(f'(x)=3x^2-6x+3m\)
Hàm số có cực trị khi f'(x) = 0 có 2 nghiệm
\(\Delta '>0\Leftrightarrow 9-9m>0\)
\(\Leftrightarrow m<1\)
\(f(x)=(\frac{1}{3}x-\frac{1}{3}) \ f'(x)+(2m-2)x+4m+4\)
f(x _{cực trị})= (2m-2)x _{cực trị}  +4m+4
phương trình đường thẳng đi qua các cực trị của đồ thị hàm số là 
\(y=(2m-2)x+4m+4 \ \ (\Delta )\)
\(A\in \Delta \Leftrightarrow 4=(2m-2)+4m+4\)
\(\Leftrightarrow 6m+2=4\)
\(\Leftrightarrow m=\frac{1}{3}\) (thỏa mãn)