Bài 1: Mặt nón - hình nón - khối nón

1. Lý thuyết:
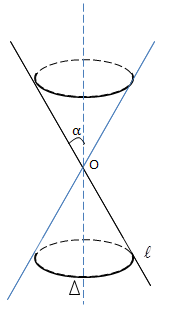
a. Mặt nón:
Giả sử $\Delta ,l$ cắt nhau $(\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ})$
Cho $l$ quay quanh $\Delta$ ta được mặt nón tròn xoay
$l:$ đường sinh
$\Delta :$ trục
$O=l\cap \Delta :$ đỉnh
$2\alpha :$ góc ở đỉnh

b. Hình nón:
Cắt mặt nón tròn xoay đỉnh O, trục $\Delta$ bởi mp (P), $(P)\perp \Delta ,O\notin (P).$ Hình giới hạn bởi mặt nón, (P) là hình nón.

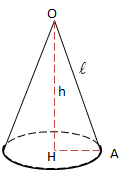
Nhận xét: Có thể xem hình nón là hình tròn xoay tạo thành khi cho đường gấp khúc $OAH ( OH\perp AH \, \, tai \, \, H)$ quay quanh  OH.
c. Khối nón:
Cho hình nón có đường sinh L, chiều cao h, bán kính đáy là R.
$V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h$
$S_{xq}=\pi Rl$
$S_{tp}=\pi Rl+\pi R^{2}$
Ví dụ 1: Phát biểu nào sau đây là đúng
A. Cho đường thẳng $l$ quay quanh $\Delta$ ta được mặt nón.
B. Cho đường thẳng  $l$ quay quanh $\Delta$, $l$ và $\Delta$ cắt nhau ta được 1 mặt nón.
C. Cho đường thẳng  $l$ quay quanh $\Delta$, $0^{\circ}<(\widehat{l,\Delta })< 90^{\circ}$ ta được 1 hình nón.
D. Cho đường thẳng  $l$ quay quanh $\Delta$, $0^{\circ}<(\widehat{l,\Delta })< 90^{\circ}$ ta được 1 mặt nón.
 Đáp án là D.
Ví dụ 2: Phát biểu nào sau đây là đúng
Cho $\Delta ABC$ vuông tại A.
A. Cho  $\Delta ABC$ quay quanh AC, ta được 1 mặt nón.
B. Cho $\Delta ABC$ quay quanh BC, ta được 1 hình nón.
C. Cho đường gấp khúc CBA quay quanh AC ta được 1 hình nón.
D. Cho đường gấp khúc CBA quay quanh AB ta được 1 khối nón.
 Đáp án là C.