GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Sơ đồ bài toán khảo sát và sẽ đồ thị hàm số
1. Tập xác định
- Nêu thêm tính chẵn, lẻ (nếu có)
2. Sự biến thiên
- Chiều biến thiên
Tính y', giải phương trình y'=0
Tìm cực trị
Tìm khoảng đơn điệu của hàm số
- Giới hạn, tiệm cận
Xét \(\lim_{x\rightarrow +\infty }y,\lim_{x\rightarrow -\infty }y\)
- Bảng biến thiên
3. Vẽ đồ thị
Xác định các điểm đặc biệt: giao với Ox, Oy điểm có tọa độ nguyên.
Nêu tâm đối xứng, trục đối xứng (nếu có)
Chú ý:
1) Đồ thị hàm số bậc ba nhân \(I(x_0,f(x_0)),f''(x_0)=0\) làm tâm đối xứng.
2) Đồ thị hàm số \(\frac{b1}{b1}\) nhận giao của hai tiệm cận làm tâm đối xứng.
3) Đồ thị hàm số lẻ nhận O(0;0) làm tâm đối xứng.
4) Đồ thị hàm số chẵn nhận Oy làm trục đối xứng.
II. Bài tập
VD1: Khảo sát và vẽ đồ thị hàm số \(y=x^3-3x^2+4\)
Giải
TXĐ: D = R
\(y'=3x^2-6x\)
\(y'=0\Leftrightarrow 3x(x-2)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=2 \end{matrix}\)
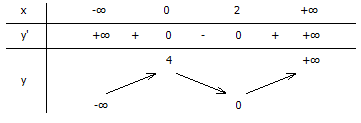
\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }x^3(1-\frac{3}{z}+\frac{4}{x^3})=+\infty\)
\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }x^3(1-\frac{3}{z}+\frac{4}{x^3})=-\infty\)
Khoảng đồng biến \((-\infty ;0);(2;+\infty )\)
Khoảng nghịch biến (0;2)
+ Hàm số đạt cực đại tại điểm x = 0; giá trị cực đại của hàm số là y = 4
+ Hàm số đạt cực tiểu tại điểm x = 2; giá trị cực tiểu của hàm số là y = 0
Giao với Ox (-1;0);(2;0)
Đi qua A(3;4)
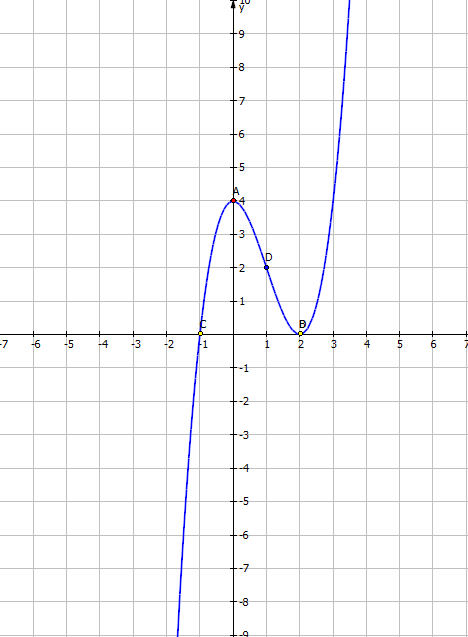
VD2: Khảo sát và vẽ đồ thị hàm số \(y=x^3+3x^2+3x+2\)
Giải
TXĐ: D = R
\(y'=3x^2+6x+3, y'=0\Leftrightarrow 3(x+1)^2=0\Leftrightarrow x=-1\)
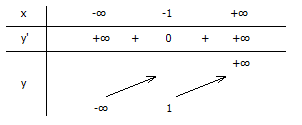
Hàm số đồng biến trên R
Hàm số không có cực trị
\(\lim_{x\rightarrow -\infty }y=-\infty,\lim_{x\rightarrow +\infty }y=+\infty\)
Giao với Oy (0;2)
Giao với Ox (-2;0)
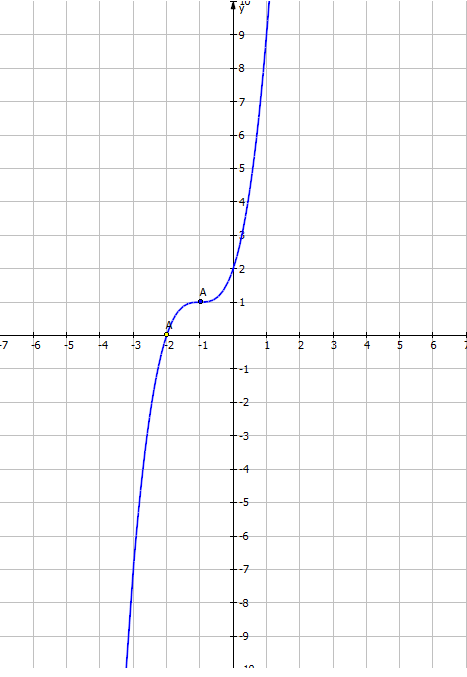
VD3: Khảo sát và vẽ đồ thị hàm số \(y=x^3+x^2+x+1\)
Giải
TXĐ: D = R
Sự biến thiên
\(y'=3x^2+3x+1>0 \ \forall x \ (do \ a = 3, \Delta '<0 )\)
Hàm số đồng biến trên R
Hàm số không có cực trị
\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }x^3(1+\frac{1}{x}+ \frac{1}{x^2}+\frac{1}{x^3})=-\infty\)
\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow -\infty }x^3(1+\frac{1}{x}+ \frac{1}{x^2}+\frac{1}{x^3})=+\infty\)
Bảng biến thiên
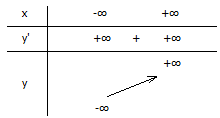
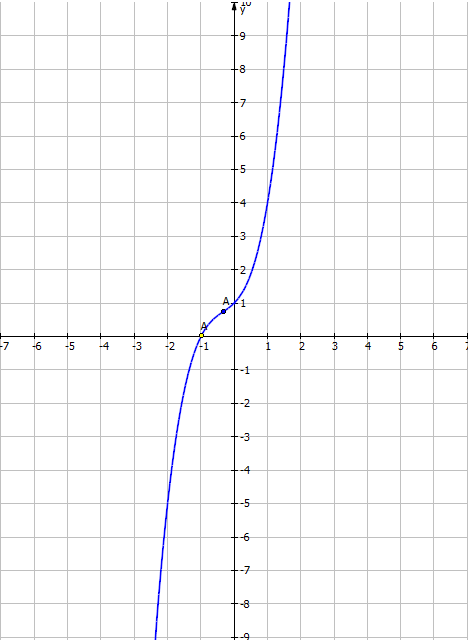
Đồ thị
Giao với Oy (0;1)
Giao với Ox (-1;0)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



