Bài 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức b1/b1

Hôm nay chúng ta sẽ học bài Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức b1/b1. Về sơ đồ bài toán khảo sát thầy đã trình bày trong bài khảo sát và vẽ đồ thị hàm số bậc 3 gồm có 3 bước:
+ TXĐ
+ Xét sự biến thiên.
+ Vẽ đồ thị.

VD1: Khảo sát và vẽ đồ thị hàm số \(y=\frac{2x+1}{x+1}\)
Giải
TXĐ: D = R \{-1}
\(y'=\frac{2(x+1)-(2x+1)}{(x+1)^2}=\frac{1}{(x+1)^2}\)
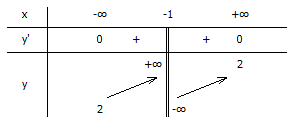
\(y'>0 \ \forall x\in (-\infty ;-1);(-1;+\infty )\)
Khoảng đồng biến \((-\infty ;-1);(-1;+\infty )\)
Hàm số không có cực trị.
Giới hạn và tiệm cận
\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{2x+1}{x+1 }=\lim_{x\rightarrow +\infty }\frac{2+\frac{1}{x}}{1+\frac{1}{x}}=2\)
Vậy đường tiệm cận ngang y - 2 = 0.
\(\lim_{x\rightarrow \infty }y=2\)
\(\lim_{x\rightarrow -1^- }y=+\infty , \lim_{x\rightarrow -1^+ }y=-\infty\)
Vậy đường tiệm cận đứng x + 1 = 0
Bảng biến thiên

Giao với Ox \((-\frac{1}{2};0)\)
Giao với Oy (0;1)
 
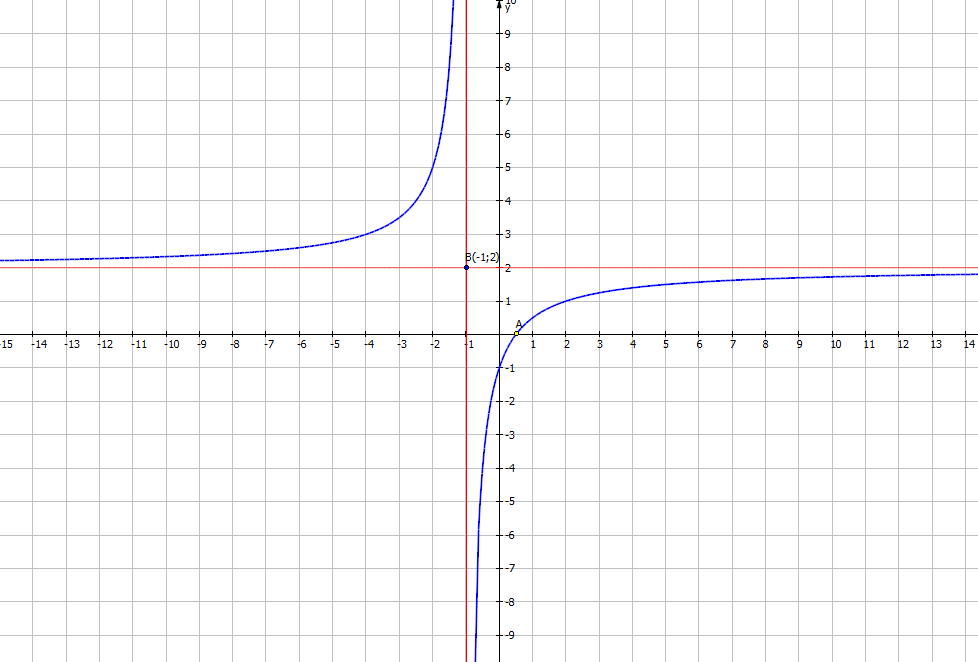
Đồ thị nhận (-1;2) làm tâm đối xứng

VD2: Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=\frac{-x+3}{x-1}\)
Giải
TXĐ: D = R\ {1}
\(y'=\frac{-(x-1)-(x+3)}{(x-1)^2}=\frac{-2}{(x-1)^2}\)
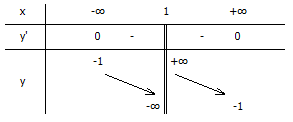
\(y'<0 \ \forall x\in (-\infty ;1),(1;+\infty )\) nên hàm số nghịch biến trên \((-\infty ;1),(1;+\infty )\)
Hàm số không có cực trị.
Giới hạn:
\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty } \frac{-x+3}{x-1}=\lim_{x\rightarrow -\infty }\frac{-1+\frac{3}{x}}{1-\frac{1}{x}} =-1\)
\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty } \frac{-x+3}{x-1}=\lim_{x\rightarrow +\infty }\frac{-1+\frac{3}{x}}{1-\frac{1}{x}} =-1\)
Đường tiệm cận ngang y + 1 = 0
 \(\lim_{x\rightarrow 1^-}y=-\infty; \lim_{x\rightarrow 1^+}y=+\infty\)
Đường tiệm cận đứng x - 1 = 0.
Bảng biến thiên

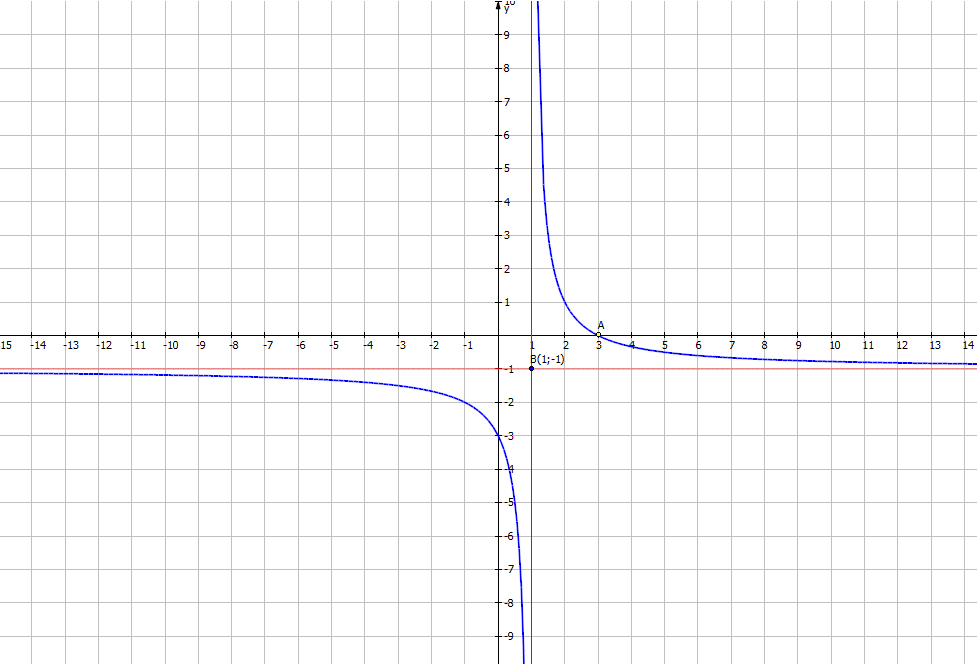
Giao với Ox (3;0)
Giao với Oy (0;-3)