Bài 2: Tìm tham số để hàm số đơn điệu trên một miền

Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm tham số để hàm số đơn điệu trên một miền như:

• Công thức tính.
• Điều kiện đủ để hàm số đơn điệu trên một miền.

Trong bài học hôm nay chúng ta sẽ học bài toán là Tìm tham số để hàm số đơn điệu trên một miền, để phục vụ cho việc giải bài toán này chúng cần thêm kiến thức sau đây.

\(I. \ f(x)=ax^2+bx+c \ \ (a\neq 0)\)

\(f(x)\geqslant 0\forall x\in R\Leftrightarrow \left\{\begin{matrix} a>0\\ \Delta \leqslant 0 \end{matrix}\right.\)
\(f(x)\leqslant 0\forall x\in R\Leftrightarrow \left\{\begin{matrix} a<0\\ \Delta \leqslant 0 \end{matrix}\right.\)
VD1: Tìm m để hàm số \(f(x)= x^3+(m-1)x^2+(m^2-4)x+9\) đồng biến trên R.
Giải
TXĐ: D = R
\(f'(x)= 3x^2+2(m-1)x+ m^2 - 4\)
f'(x) = 0 tối đa 2 nghiệm
Để hàm số đồng biến trên R thì \(f(x)\geqslant 0 \ \forall x\in R\)
\(\Leftrightarrow \left\{\begin{matrix} 3>0\\ \Delta '=(m-1)^2-3(m^2-4)\leq 0 \end{matrix}\right.\)
\(\Leftrightarrow m^2-2m+1-3m^2+12\leq 0\)
\(\Leftrightarrow -2m^2-2m+13\leq 0\)
\(-2m^2-2m+13=0\Leftrightarrow 2m^2+2m-13=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} m=\frac{1-3\sqrt{3}}{2}\\ m=\frac{1+3\sqrt{3}}{2} \end{matrix}\)
KL: \(\bigg \lbrack\begin{matrix} m\leq \frac{1-3\sqrt{3}}{2}\\ m\geq \frac{1+3\sqrt{3}}{2} \end{matrix}\)
VD2: Tìm m để hàm số \(f(x)=[(m^2-2m)\frac{x^2}{3}+mx+3]\) đồng biến trên R
Giải 
TXĐ: D = R
\(f'(x)=(m^2-2m)\frac{x^3}{3}+mx^2+3x\)
\(f'(x)=(m^2-2m)x^2+2mx+3\)
TH1: \(m^2-2m=0\Leftrightarrow \begin{bmatrix} m=0\\ m=2 \end{matrix}\)
\(m=0, f(x)=3>0\forall x\in R\)  hàm số đồng biến trên R

\(m=2, f(x)=4x+3, f'(x)\geqslant 0\Leftrightarrow x\geqslant -\frac{3}{4}\)  m=2 (không thỏa mãn)
TH2: \(m^2-2m\neq 0\)
f'(x) là tam thức bậc hai có tối đa 2 nghiệm 
Hàm số đồng biến trên R khi  \(f(x)\geq 0 \ \forall x\in R\)
\(\left\{\begin{matrix} m^2-2m>0\\ \Delta '=m^2-3(m^2-2m)\leq 0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m^2-2m>0\\ -2m^2+6m\leq 0 \end{matrix}\right.\)
VD3: Tìm m để hàm số \(f(x)=-x^3+3x^2+3mx-1\) nghịch biến trên \((0;+\infty )\)
Giải
TXĐ: D = R
\(f'(x)=-3x^2+6x+3m\)
f(x) là tam thức b2, f(x) = 0 có tối đa 2 nghiệm
Để hàm số nghịch biến trên  thì
\(f'(x)\leq 0, \forall x\in (0;+\infty )\)
\(\Leftrightarrow -3x^2+6x+3m\leq 0 \ \ \forall x\in (0;+\infty )\)
\(\Leftrightarrow m\leq x^2-2x \ \ \forall x\in (0;+\infty )\)
Xét \(g(x)=x^2-2x\) trên \((0;+\infty )\)
\(g'(x)=2x-2, \ g'(x)=0\Leftrightarrow x=1\)

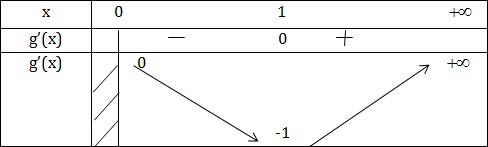
KL: \(m\leq -1\)
VD4: Tìm m để hàm số \(f(x)=\frac{3mx+1}{x-2}\)
a) Nghịch biến trên các khoảng  \((-\infty ;2),(2;+\infty )\)
​b) Đồng biến trên các khoảng \((-\infty ;2),(2;+\infty )\)
Giải
a) D=R \ {2}
\(f'(x)=\frac{3m(x-2)-(3mx+1)}{(x-2)^2}\)
\(=\frac{-6m-1}{(x-2)^2}\)
TH1: \(-6m-1=0\Leftrightarrow m=-\frac{1}{6}\)
Khi đó  \(f(x)=0 \ \forall x\neq 2\)
Hàm số \(f(x)=-\frac{1}{2} \ \forall x\neq 2\)

Hàm số không đồng biến, nghịch biến trên \((-\infty ;2),(2;+\infty )\)
TH2: \(-6m-1\neq 0\Leftrightarrow m\neq -\frac{1}{6}\)
Hàm số nghịch biến\((-\infty ;2),(2;+\infty )\) thì \(f'(x)<0\forall x\neq 2\Leftrightarrow -6m-1<0\)
\(\Leftrightarrow -6m<1\)
\(\Leftrightarrow m> -\frac{1}{6}\)
KL: \(m> -\frac{1}{6}\)
b)
TH1: \(-6m-1=0\Leftrightarrow m=-\frac{1}{6}\)
(tương tự a) \(m=-\frac{1}{6}\) ( không thỏa mãn)
TH2: \(-6m-1\neq 0\Leftrightarrow m=\neq -\frac{1}{6}\)

Hàm số đồng biến trên \((-\infty ;2),(2;+\infty )\) khi \(f'(x)>0 \ \forall x\neq 2\Leftrightarrow -6m-1>0\)
\(\Leftrightarrow -6m>1\)
\(\Leftrightarrow m< -\frac{1}{6}\)
KL: \(m< -\frac{1}{6}\)