Bài 22: Bài toán về vị trí tương đối giữa mặt cầu và đường thẳng

I. Lý thuyết 
Cho mặt cầu (S) tâm I, bán kính R và đường thẳng \(\Delta\) (đi qua M, có 1 VTCP \(\vec{u}\))
TH1:
d(I; \(\Delta\)) > R thì \(\Delta \cap (S)= \varnothing\)

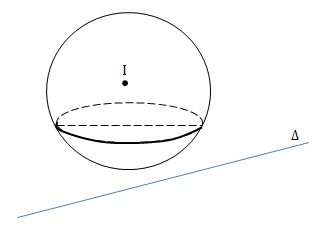
TH2:
\(d(I;\Delta )=R\)
\(\Delta \cap (S)={H}\)
\(\Delta\): Tiếp tuyến
H: Tiếp điểm

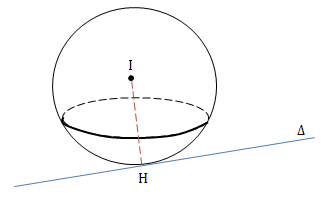
TH3:
\(d(I;\Delta )<R\) thì \(\Delta \cap (S)=\left \{ A;B \right \}\)
\(R^2=d^2(I;\Delta )+\frac{AB^2}{4}\)
\(AB=2.\sqrt{R^2-d^2(I;\Delta )}\)

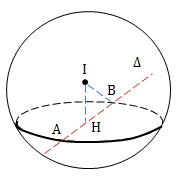
II. Bài tập
VD1: Cho mặt cầu (S) \((x+2)^2+(y-1)^2+(z+5)^2=109\) và đường thẳng \(\Delta:\left\{\begin{matrix} x=-5+3t\\ y=-1+5t\\ z=9-4t \end{matrix}\right.\)
a) CMR \(\Delta\) cắt mặt cầu (S) tại 2 điểm
b) Tìm tọa độ các giao điểm đó
Giải

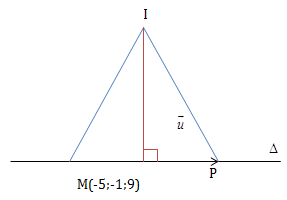
a)
(S) có tâm I(-2;1;-5), bán kính R = \(\sqrt{109}\)
\(d(I;\Delta )=\frac{\left | [\overrightarrow{MI};\vec{u}] \right |}{\left | \vec{u} \right |}\)
Trong đó \(\vec{u}=(3;5;-4), M(-5;-1;9)\)
\(\begin{matrix} \overrightarrow{MI}=(3;2;-14)\\ \vec{u}=(3;5;-4) \ \ \ \ \end{matrix}\)
\([\overrightarrow{MI};\vec{u}]=\left ( \begin{vmatrix} 2 \ \ -14\\ 5 \ \ -4 \end{vmatrix};\begin{vmatrix} -14 \ \ 3\\ -4 \ \ 3 \end{vmatrix};\begin{vmatrix} 3 \ \ 2\\ 3 \ \ 5 \end{vmatrix} \right )=(62;-30;9)\)
\(d(I;\Delta )=\frac{\left | [\overrightarrow{MI};\vec{u}] \right |}{\vec{u}}= \frac{\sqrt{62^2+(-30)^2+9^2}}{\sqrt{3^2+5^2+(-4)^2}}< R=\sqrt{109}\)
Vậy \(\Delta\) cắt (S) tại 2 điểm phân biệt
b)
A là một giao điểm \(\Delta\) và (S)
\(A\in \Delta\Rightarrow A(-5+3t;-1+5t;9-4t)\)
\(A\in (S)\Rightarrow (-3+3t^2)+(5t-2)^2+(14-4t)=109\)
\(\Leftrightarrow 50t^2-150t+209=109\)
\(\Leftrightarrow 50t^2-150t+100=0\)
\(\Leftrightarrow t^2-3t+2=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} t=1\\ t=2 \end{matrix}\)
t = 1 ta có A(-2;4;5)
t = 2 ta có B(1;9;1)
VD2: Viết phương trình mặt cầu (S) tâm I(1;2;3) và tiếp xúc với đường thẳng \(\Delta :\frac{x}{2}=\frac{y+1}{1}=\frac{z-1}{2}\)
Giải


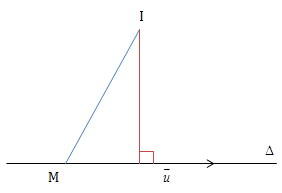
\(\Delta\) tiếp xúc (S) ⇔ d(I; \(\Delta\)) = R
\(\Delta\) đi qua M (0;-1;1), có VTCP \(\vec{u}\) =(2;1;2)
\(\overrightarrow{MI}=(1;3;2)\)
\(\overrightarrow{u}=(2;1;2)\)
\(R=d(I;\Delta )=\frac{\left | [\overrightarrow{MI};\vec{u}] \right |}{\left | \vec{u} \right |}\)
\([\overrightarrow{MI};\vec{u}]=\left ( \begin{vmatrix} 3 \ \ \ 2\\ 1 \ \ \ 2 \end{vmatrix};\begin{vmatrix} 2 \ \ \ 1\\ 2 \ \ \ 2 \end{vmatrix};\begin{vmatrix} 1 \ \ \ 3\\ 2 \ \ \ 1 \end{vmatrix} \right )=(4;2;-5)\)\(d(I;\Delta )=\frac{\sqrt{4^2+262+(-5^2)}}{\sqrt{2^2+1^2+2^2}}=\frac{3\sqrt{5}}{3}=\sqrt{5}\)
\(\Rightarrow R=\sqrt{5}\)
Phương trình mặt cầu \((x-1)^2+(y-2)^2+(z-3)^2=5\)
VD3: Cho đường thẳng  \(\Delta\) là giao tuyến của hai mặt phẳng 
\(\begin{matrix} (\alpha ): 5x-4y+3z+20=0\\ (\beta ): 3x-4y+z-8=0 \ \ \ \ \end{matrix}\)
Viết phương trình mặt cầu có tâm I(2.3;1) và cắt \(\Delta\) tại hai điểm AB sao cho AB =16
Giải

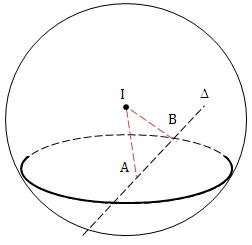
\(\Delta \cap (S)=\left \{ A;B \right \}\)
\(AB=2\sqrt{R^2-d^2(I;\Delta )}\)
\(\Rightarrow R^2=\left ( \frac{AB}{2} \right )^2+d^2(I;\Delta )=64+d^2(I;\Delta ) \ (1)\)
* Viết phương trình tham số của \(\Delta\)
Đặt x = t

\(-\begin{matrix} 5t-4y+3z+20=0 \ \ \ \\ 3t-4y+z-5=0 \ \ (2) \end{matrix}\)
\(2t+2z+28=0\Rightarrow z=-14-t\)
Từ (2) 
\(4y=3t+z-8=2t-22\)
\(y=-\frac{11}{2}+\frac{1}{2}t\)
\(pt \ \Delta \left\{\begin{matrix} x=t\\ y=-\frac{11}{2}+\frac{1}{2}t\\ z=-14-t \end{matrix}\right.\)
đi qua \(M(0;-\frac{11}{2};-14)\)
có \(\vec{u}=(1;\frac{1}{2};-1)\)
\(\overrightarrow{MI}=(2;\frac{17}{2};13)\)
\(\vec{u}=(1;\frac{1}{2};-1)\)
\(\left [ \overrightarrow{MI};\vec{u} \right ]= \left ( \begin{vmatrix} \frac{17}{2} \ \ \ 13\\ \\ \frac{1}{2} \ \ \ -1 \end{vmatrix}; \begin{vmatrix} 13 \ \ \ 2\\ \\ -1 \ \ \ 1 \end{vmatrix};\begin{vmatrix} 2\ \ \ \frac{17}{2} \\ \\ 1 \ \ \ \frac{1}{2} \end{vmatrix} \right )=(-15;15;-\frac{15}{2})\)
\(d(I;\Delta )=\frac{\left | \left [ \overrightarrow{MI};\vec{u} \right ] \right |}{\left | \vec{u } \right |}=\frac{\sqrt{(-15)^2+15^2+(-\frac{15}{2})}}{\sqrt{1^2+(\frac{1}{2})^2+(-1)^2 }}\)
\(=\frac{15.\sqrt{1^2+1^2+(\frac{1}{2})^2}}{\sqrt{1^2+1^2+(\frac{1}{2})^2}}=15\)
Từ (1)
\(R^2=64+225=289\)
Phương trình mặt cầu
\((x-2)^2+(y-3)^2+(z+1)^2=289\)