Bài 7: Ứng dụng tích có hướng tính diện tích

I. Lý thuyết
\(\vec{a}=(x_1;y_1;z_1)\)
\(\vec{b}=(x_2;y_2;z_2)\)
\(\left [ \vec{a}; \vec{b} \right ]= \left ( \begin{vmatrix} y_1 \ \ z_1\\ y_2 \ \ z_2 \end{vmatrix}; \begin{vmatrix} z_1 \ \ x_1\\ z_2 \ \ x_2 \end{vmatrix}; \begin{vmatrix} x_1 \ \ y_1\\ x_2 \ \ y_2 \end{vmatrix} \right )\)
\(\left | \left [ \vec{a}; \vec{b} \right ] \right |= \left | \vec{a} \right |.\left | \vec{b} \right |.sin(\vec{a};\vec{b})\)
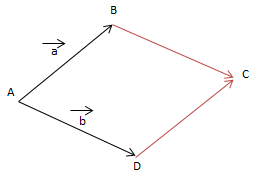
1) ABCD là hình bình hành
\(S_{ABCD}=\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\)
2) \(\Delta ABC\)
\(S_{\Delta ABC}=\frac{1}{2}\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\)

II. Bài tập
VD1: Cho \(\Delta ABC\), A(-1;0;2), B(1;-2;3), C(0;1;-1)
a) Tính S_ABC
b) Tính độ dài đường cao AH của  \(\Delta ABC\)
Giải
a)
\(\overrightarrow{AB} =(2;-2;1)\)
\(\overrightarrow{AC} =(1;1;-3)\)
\(\left [ \overrightarrow{AB}; \overrightarrow{AC} \right ]= \left ( \begin{vmatrix} -2 \ \ 1\\ 1 \ \ -3 \end{vmatrix}; \begin{vmatrix} 1 \ \ 2\\ -3 \ \ 1 \end{vmatrix}; \begin{vmatrix} 2 \ \ -2\\ 1 \ \ 1 \end{vmatrix} \right )=(5;7;4)\)
\(S_{ABC}=\frac{1}{2}\left | \left [ \overrightarrow{AB}; \overrightarrow{AC} \right ] \right |= \frac{1}{2} \sqrt{5^2+7^2+4^2}=\frac{1}{2}\sqrt{90}=\frac{3}{2}\sqrt{10}\)
b)
\(BC=\sqrt{(0-1)^2+(1+2)^2+(-1-3)^2}=\sqrt{26}\)
\(AH=\frac{2S_{ABC}}{BC}=\frac{3\sqrt{10}}{\sqrt{26}}\)
\(\frac{3\sqrt{5}}{\sqrt{13}}=\frac{3.\sqrt{65}}{13}\)
VD2: Cho A(1;2;-1), B(-2;1;3). Tìm M \(\in\) Ox sao cho
a) \(S_{\Delta MAB}=10\)
b) \(S_{\Delta MAB}\) nhỏ nhất
Giải
a)
M \(\in\) Ox ⇒ M(m;0;0)
\(\overrightarrow{AB}=(-3;-1;4)\)
\(\overrightarrow{AM}=(m-1;-2;1)\)
\(\left [ \overrightarrow{AB};\overrightarrow{AM} \right ]= \left ( \begin{vmatrix} -1 \ \ -4\\ -2 \ \ 1 \end{vmatrix}; \begin{vmatrix} 4 \ \ -3\\ 1 \ \ m-1 \end{vmatrix}; \begin{vmatrix} -3 \ \ -1\\ m-1 \ \ -2 \end{vmatrix} \right )\)\(= (7;4m-1;m+5)\)
\(S_{\Delta MAB}=\frac{1}{2}\left | \left [ \overrightarrow{AB}; \overrightarrow{AM} \right ] \right |= \frac{1}{2}\sqrt{49+(4m-1)^2+(m+5)^2}\)
\(= \frac{1}{2}\sqrt{15m^2+2m+75}\)
\(S_{\Delta MAB}=10\Leftrightarrow \frac{1}{2}\sqrt{15m^2+2m+75}=10\)
\(\Leftrightarrow 17m^2+2m+75=400\)
\(\Leftrightarrow 17m^2+2m-325=0\)
\(\Delta '=1+17.325=5525\)
\(\Bigg \lbrack\begin{matrix} m=\frac{-1-\sqrt{5525}}{17}\rightarrow M_1\left ( \frac{-1-\sqrt{5525}}{17};0;0 \right )\\ \\ m=\frac{-1+\sqrt{5525}}{17}\rightarrow M_2 \left ( \frac{-1+\sqrt{5525}}{17};0;0 \right ) \end{matrix}\)
b)
\(S_{MAB}\) min khi và chỉ khi
\(17m^2+2m+75 \ \ min\)
Ta có \(T=17m^2+2m+75=17\left [ m^2+2.m.\frac{1}{17}+\frac{1}{289} \right ]+75-\frac{1}{17}\)
\(=17\left ( m+\frac{1}{17} \right )^2+\frac{1275}{17}\geq \frac{1275}{17}\)
\(T_{min}\Leftrightarrow m=-\frac{1}{17}\)
Vậy \(M(-\frac{1}{17};0;0)\)