Bài 13: Bài toán xác định điểm liên quan đến mặt phẳng

VD1: Trong không gian với hệ tọa độ Oxyz cho A(3;0;-1), B(1;3;-2), C(3;-4;1). Tìm N thuộc (Oyz) sao cho NA = NB = NC.
Giải
(Oyz) đi qua O(0;0;0) có 1 VTPT
\(\vec{i}=(1;0;0)\) nên có pt: x = 0
\(N\in (Oyz)\Rightarrow N(o;b;c)\)
\(\left\{\begin{matrix} NA=NB\\ NA=NC \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} NA^2=NB^2\\ NA^2=NC^2 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (0-3)^2+(b-0)^2+(c+1)^2=(0-1)^2+(b-3)^2+(c+2)^2\\ (0-3)^2+(b-0)^2+(c+1)^2=(0-3)^2+(b+4)^2+(c-1)^2 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 9+b^2+c^2+2c+1=1+b^2-6b+9+c^2+4c+4\\ 9+b^2+c^2+2c+1=9+b^2+8b+16+c^2-2c+1 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} 6b-2c=4\\ 8b-4c=-16 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3b-c=2\\ 2b-c=-4 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b=6\\ c=16 \end{matrix}\right.\)
Vậy N(0;6;16)
VD2: Trong không gian với hệ tọa độ Oxyz cho A(2;3;1), B(0;-1;2), C(1;0;3). Tìm tọa độ điểm P thuộc (Oxy) sao cho
\(a) \ \left | \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} \right | \ \ {min}\)
\(b) \ PA^2+PB^2+PC^2 \ \ min\)
Giải
(Oxy) đi qua O và có 1 VTPT \(\vec{k}=(0;0;1)\)
pt (Oxy): z = 0 
\(P\in (Oxy)\Rightarrow P(a;b;0)\)
a) G là điểm sao cho \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\left\{\begin{matrix} x_G=\frac{1}{3}(x_A+x_B+x_C)=\frac{1}{3}(2+0+1)=1 \ \ \\ y_G=\frac{1}{3}(y_A+y_B+y_C)=\frac{1}{3}(3+(-1)+0)=\frac{2}{3}\\ z_G=\frac{1}{3}(z_A+z_B+z_C)=\frac{1}{3}(1+2+3)=2 \ \ \ \ \ \ \end{matrix}\right.\)
\(G(1;\frac{2}{3};2)\)
Cách 1:
\(\left | \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} \right | =\left | 3\overrightarrow{PG} \right |=3PG\)
\(\left | \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} \right | \ \ {min}\Leftrightarrow PG \ min\)
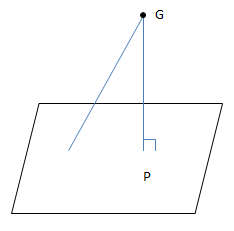
⇔ P là hình chiếu của G lên (Oxy)
\(\Leftrightarrow P(1;\frac{2}{3};0)\)

Cách 2:
\(\overrightarrow{PA}=(2-a;3-b;1)\)
\(\overrightarrow{PB}=(-a;-1-b;2)\)
\(\overrightarrow{PC}=(1-a;-b;3)\)
\(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} = (3-3a;2-3b;6)\)
\(\left | \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} \right |= \sqrt{(3-3a)^2+(2-3b)^2+6^2}\geq 6\)
\(\left | \overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC} \right | _{min}= 6\Leftrightarrow \left\{\begin{matrix} 3-3a=0\\ 2-3b=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=\frac{2}{3} \end{matrix}\right.\)
Vậy \(P(1;\frac{2}{3};0)\)
b)
Cách 1:
\(T=PA^2+PB^2+PC^2=\overrightarrow{PA}^2+\overrightarrow{PB}^2+ \overrightarrow{PC}^2\)
\(=(\overrightarrow{PG}+\overrightarrow{GA})^2+ (\overrightarrow{PG}+\overrightarrow{GB})^2+ (\overrightarrow{PG}+\overrightarrow{GC})^2\)
\(=PG^2+2\overrightarrow{PG}.\overrightarrow{GA}+GA^2+PG^2+ 2\overrightarrow{PG}.\overrightarrow{GB}+GB^2+PG^2+2 \overrightarrow{PG}.\overrightarrow{GC}+GC^2\)
\(=3PG^2+2\overrightarrow{PG}\underset{\overrightarrow{0}}{(\overrightarrow{GA}+\overrightarrow{GB}+ \overrightarrow{GC})}+GA^2+GB^2+GC^2\)
\(=3PG^2+\underset{0 \ doi}{GA^2+GB^2+GC^2}\)
\(T_{min}\Leftrightarrow 3PG^2_{min}\) mà \(P \in(Oxy)\) nên P là hình chiếu của G trên (Oxy)
Suy ra \(P(1;\frac{2}{3};0)\)
Cách 2:
\(PA^2=(2-a)^2+(3-b)^2+1=a^2+b^2-4a-6b+14\)
\(PB^2=(-a)^2+(-1-b)^2+2^2=a^2+b^2+2b+5\)
\(PC^2=(1-a)^2+(-b)^^2+3^2=a^2+b^2-2a+10\)
\(PA^2+PB^2+PC^2=3a^2-6a+3b^2-4b+29\)
\(=3(a^2-2a+1)+3(b^2-\frac{4}{3}b+\frac{4}{9})+\frac{223}{9}\)
\(=3(a-1)^2+3(b-\frac{2}{3})^2+\frac{223}{9}\geq \frac{223}{9}\)
\(T_{min}=\frac{223}{9} \ khi \ \left\{\begin{matrix} a=1\\ b=\frac{2}{3} \end{matrix}\right.\)
Vậy \(P(1;\frac{2}{3};0)\)
VD3: Trong không gian với hệ tọa độ Oxyz, cho A(2;3;1), B(0;0;2), C(1;0;3). Tìm điểm M trên (Oxz) sao cho \(\left | \overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC} \right |_{min}\)
Giải
Cách 1:
Gọi I(a;b;c) là điểm sao cho \(\overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(\overrightarrow{IA}=(2-a;3-b;1-c)\)
\(\overrightarrow{IB}=(-a;-b;2-c)\Rightarrow 2\overrightarrow{IB}=(-2a;-2b;4-2c)\)
\(\overrightarrow{IC}=(1-a;-b;3-c)\Rightarrow 3\overrightarrow{IC}=(3-3a;-3b;9-3c)\)
\(\overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC} =(5-6a;3-6b;14-6c)\)
\(\overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC} =\overrightarrow{0}\Leftrightarrow \left\{\begin{matrix} 5-6a=0\\ 3-6b=0\\ 14-6c=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{5}{6}\\ \\ b=\frac{1}{2}\\ \\c=\frac{7}{3} \end{matrix}\right.\)
\(I(\frac{5}{6};\frac{1}{2};\frac{7}{3})\)
\(\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC} =\overrightarrow{MI}+\overrightarrow{IA}+2(\overrightarrow{MI}+\overrightarrow{IB} )+3(\overrightarrow{MI}+\overrightarrow{IC})\)
\(=6\overrightarrow{MI}+\overrightarrow{IA}+2\overrightarrow{IB}+3\overrightarrow{IC}=6\overrightarrow{MI}\)
\(T=\left | \overrightarrow{MA}+2\overrightarrow{MB}+3 \overrightarrow{MC} \right |=6MI\)
T_min ⇔ MI min, mà \(M\in (Oxz)\)
nên M là hình chiếu của I trên (Oxz) hay \(M(\frac{5}{6};0;\frac{7}{3})\)
Cách 2:
\(M\in (Oxz)\Rightarrow M(a;0;c)\)
\(\overrightarrow{MA}=(2-a;3;1-c)\)
\(\overrightarrow{MB}=(-a;0;2-c)\Rightarrow 2\overrightarrow{MB} =(-2a;0;4-2c)\)
\(\overrightarrow{MC}=(1-a;0;3-c)\Rightarrow 3\overrightarrow{MC} =(3-3a;0;9-3c)\)
\(\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}=( 5-6a;3,14-6c)\)
\(T=\left | \overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC} \right |=\sqrt{(5-6a)^2+9+(14-6c)^2}\geq 9\)
\(T_{min}=9\Leftrightarrow \left\{\begin{matrix} 5-6a=0\\ 14-6c=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{5}{6}\\ \\ c=\frac{7}{3} \end{matrix}\right.\)
Vậy \(M(\frac{5}{6};0;\frac{7}{3})\)
Chú ý: 
Nếu \(x\overrightarrow{IA}+y\overrightarrow{IB}+z\overrightarrow{IC}=\overrightarrow{0}\)
Thì \(x\overrightarrow{MA}+y\overrightarrow{MB}+z\overrightarrow{MC}= (x+y+z).\overrightarrow{MI}\)