Bài 1: Lũy thừa

I. Lũy Thừa
a) a > 0
\(a^x.a^y=a^{x+y} \ \ \ x, y\in \mathbb{R}\)
\(\frac{a^x}{a^y}=a^{x-y} \ \ \ x, y \in \mathbb{R}\)
\((a^x)^y=a^{xy} \ \ \ x,y\in R\)
\(\sqrt[x]{a^y}=a^{\frac{y}{x}} \ \ \ x\in N, x\geq 2, y\in R\)
\((a.b)^x=a^x.b^x\)
\(\left ( \frac{a}{b} \right )^y=\frac{a^y}{b^y}\)
Chú ý: \(a^{\circ}=1, \ \ \ 0<a\)

b)
\(a>1 \ \ \ a^x > a^y\Leftrightarrow x>y\)
\(0<a<1 \ \ \ a^x > a^y\Leftrightarrow x<y\)
II. Hàm số mũ
Dạng: \(y=a^x \ \ \ 0 < a \neq 1\)
TXĐ: R
TGT: \((0;+\infty )\)
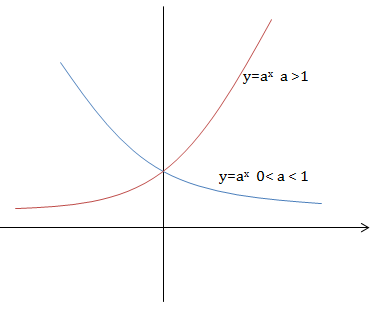
a > 1 HS \(y=a^x\) đồng biến trên R
0 < a < 1 hàm số nghịch biến trên R

Đạo hàm
\((a^x)'=a^x.lna. \ \ \ 0<a\neq 1\)
\((e^x)'=e^x.\)
\(2^?=8\)
\(2^x=3\rightarrow x=log_23\)
III. Bài tập
VD1: Rút gọn 
\(A=\sqrt{2\sqrt{2\sqrt{2\sqrt{2}}}}\)
Giải
Cách 1:
\(A=2^{\frac{1}{2}}.2^{\frac{1}{4}}.2^{\frac{1}{8}}.2^{\frac{1}{16}}\)
\(A=2^{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}}=2^\frac{15}{16}\)
Cách 2:
\(A=\sqrt{2.\sqrt{2.\sqrt{2.2^\frac{1}{2}}}}\)
\(=\sqrt{2.\sqrt{2.\sqrt{2^\frac{3}{2}}}}\)
\(=\sqrt{2.\sqrt{2.2^\frac{3}{4}}}\)
\(=\sqrt{2.\sqrt{2^\frac{7}{4}}}\)
\(=\sqrt{2.2^\frac{7}{8}}\)
\(=\sqrt{2^\frac{15}{8}}=2^\frac{15}{16}\)

VD2: Rút gọn
\(B=0,125.\sqrt[3]{0,25}.\sqrt{2\sqrt{2}}\)
Giải
\(=2^{-3}.\sqrt[3]{2^{-2}}.2^\frac{1}{2}.2^\frac{1}{4}\)
\(=2^{-3}.2^{-\frac{2}{3}}.2^\frac{1}{2}.2^\frac{1}{4}\)
\(=2^{-3-\frac{2}{3}+\frac{1}{2}+\frac{1}{4}}=2^{-\frac{35}{12}}\)
VD3: Xét tính đồng biến, nghịch biến của hàm số sau: 
a) \(y=(\sqrt{10}-3)^x\)
b) \(y=(\sqrt{10}-3)^{-2x}\)
Giải
a)
Giải \(0< \sqrt{10}-3<1\) nên hàm số nghịch biến trên R
b)

\(y=\left [ \frac{1}{(\sqrt{10-3})^2} \right ]^x\)
Ta có
\(\frac{1}{(\sqrt{10-3})^2} =(\sqrt{10-3})^2>1\)
Vậy hàm số đồng biến trên R
VD4: Tính đạo hàm các hàm số sau:
\(a) \ \ y = 2^x+3^{x^2}\)
\(a) \ \ y = e^x+e^{x^2+2x}\)
Giải
a) 
\(y'=2^x.lnx+(x^2)'.3^{x^2}.ln3\)
\(=2^x.lnx+2x.3^{x^2}.ln3\)
b)
\(y'=e^x+(x^2+2x)'.e^{x^2+2x}\)
\(=e^x+(2x+2).e^{x^2+2x}\)
Chú ý:
\((a^x)'=a^x.lna\)
\((a^u)'=u'.a^u.lna\)
\((e^x)'=e^x\)
\((e^u)'=u'.e^u\)