Bài 20: Bài toán viết phương trình mặt cầu

I. Lý thuyết 
1)
Phương trình mặt cầu tâm I(a;b;c), bán kính R
\((x-a)^2+(y-b)^2+(z-c)^2=R^2\)
2) 
\(Pt \ x^2+y^2+z^2+2Ax+2By+2Cz+D=0\)
là phương trình mặt cầu khi \(A^2+B^2+C^2-D> 0\)
Khi đó \(\left\{\begin{matrix} tam \ I(-A;-B;-C)\\ BK \ R =\sqrt{A^2+B^2+C^2-D} \end{matrix}\right.\)
2. Bài tập
VD1: Viết phương trình mặt cầu có đường kính AB, \(A(2;1;3), B(0;-3;1)\)

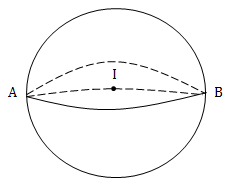
Giải
Tâm I của mặt cầu là trung điểm của AB 
I(1;-1;2)
\(BK \ R =\frac{1}{2}AB=\frac{1}{2}.\sqrt{(0-2)^2+(-3-1)^2+(1-3)^2}\)
\(=\frac{1}{2}.\sqrt{4+16+4}=\sqrt{6}\)
Phương trình mặt cầu:
\((x-1)^2+(y+1)^2+(z-2)^2=6\)
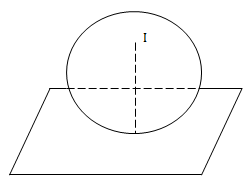
VD2: Viết phương trình mặt cầu tâm I(1;2;3) và tiếp xúc với mặt phẳng \(2x-y+2z+1=0 \ (P)\)
Giải
Mặt cầu tiếp xúc (P) nên
\(R=d(I;(P))=\frac{\left | 2-2+6+1 \right |}{\sqrt{2^2+(-1)^2+2^2}}=\frac{7}{3}\)

PT mặt cầu \((x-1)^2+(y-2)^2+(z-3)^2=\frac{49}{9}\)
VD3: Viết phương trình mặt cầu đi qua 4 điểm \(A(0;0;0), B(1;0;0), C(0;1;0),D(0;0;1)\)
Giải

Cách 1:
Gọi phương trình mặt cầu là 
\(x^2+y^2+z^2+2ax+2by+2cz+d=0 \ \ (S)\)
\(A\in (S)\Leftrightarrow d=0 \ \ \ \(1)\)
\(B\in (S)\Leftrightarrow 1+2a+d=0 \ \ (2)\)
\(C\in (S)\Leftrightarrow 1+2b+d=0 \ \ (3)\)
\(D\in (S)\Leftrightarrow 1+2c+d=0 \ \ (4)\)
Từ (1), (2) (3) (4) ta có
\(\left\{\begin{matrix} a=-\frac{1}{2}\\ b=-\frac{1}{2}\\ c=-\frac{1}{2}\\ d=0 \end{matrix}\right.\)
\(PT \ (S): x^2+y^2+z^2-x-y-z=0\)
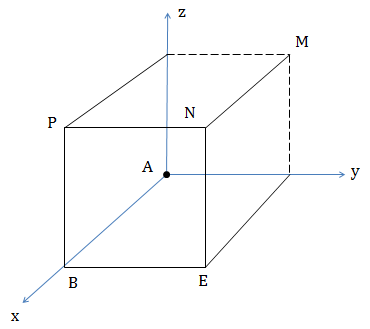
Cách 2: Dựng hình lập phương ABEC.DMNP như hình vẽ
\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\Rightarrow \overrightarrow{AN}=(1;1;1)\Rightarrow N(1;1;1)\)
ABEC.DMNP là hình lập phương nên mặt cầu đi qua A, B, C, D cũng là mặt cầu đi qua các đỉnh hình lập phương nhận AN làm đường kính.
Tâm mặt cầu là trung điểm AN 
\(I(\frac{1}{2};\frac{1}{2};\frac{1}{2})\)
\(BK \ \ R =\frac{1}{2}AN=\frac{1}{2}\sqrt{1^2+1^2+1^2}=\frac{\sqrt{3}}{2}\)