Bài 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn

Trong bài học này chúng ta sẽ học Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn. Trước hết, thầy sẽ nhắc lại sơ đồ bài toán khảo sát và vẽ đồ thị hàm số thì chúng ta có 3 bước:
+ TXĐ, nêu tính chẳn lẻ của hàm số
+ Sự biến thiên, tính đạo hàm, tìm cực trị, đồng biến nghịch biến, lập bảng biến thiên,tìm tiệm cận nếu có.
+ Vẽ đồ thị hàm số.

VD1: Khảo sát và vẽ đồ thị hàm số \(y=x^4-2x^2\)
Giải
TXĐ: D = R
\(y'=4x^3-4x\)
\(y'=0\Leftrightarrow 4x(x^2-1)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=1\\ x=-1 \end{matrix}\)

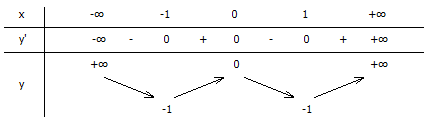
+ Hàm số đạt cực đại tại điểm x = 0; giá trị cực đại của hàm số là y = 0
+ Hàm số đạt cực tiểu tại điểm x = -1; x = 1; giá trị cực tiểu của hàm số là y = -1
Hàm số đồng biến \((-1;0);(1;+\infty )\)
Hàm số nghịch biến \((-\infty ;-1),(0;1)\)
\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }x^4(1-\frac{2}{x^2 })=+\infty\)
\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }x^4(1-\frac{2}{x^2 })=+\infty\)
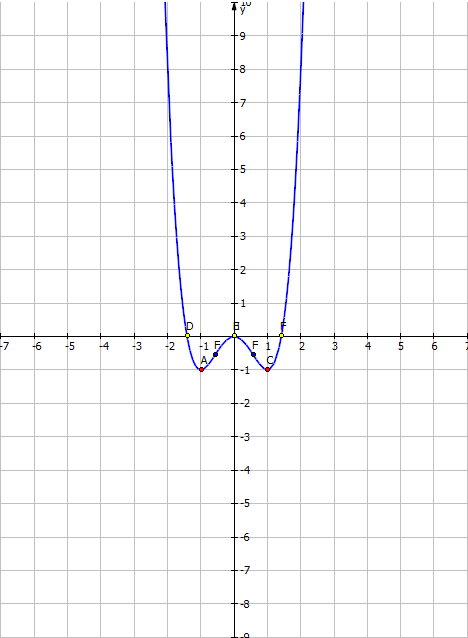
Giao với Ox \((0;0),(-\sqrt{2};0);(\sqrt{2};0)\)
Giao với Oy (0;0)
Do hàm số chẵn nên đồ thị nhận trục tung liên tục đối xứng.

VD2: Khảo sát và vẽ đồ thị hàm số \(y=-x^4-x^2-2\)
Giải
TXĐ: D = R
\(y'=-4x^3-2x\)
\(y'=0\Leftrightarrow -2x(2x^2+1)=0\Leftrightarrow x=0\)

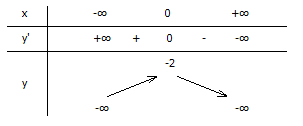
Hàm số đạt cực đại tại điểm x = 0; giá trị cực đại của hàm số là y = -2
Hàm số đồng biến trên  \((-\infty ;0)\)
Hàm số nghịch biến trên \((0;+\infty)\)
\(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow -\infty }-x^4 (1+\frac{1}{x^2}+\frac{2}{x^4})=-\infty\)\(\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }-x^4 (1+\frac{1}{x^2}+\frac{2}{x^4})=-\infty\)
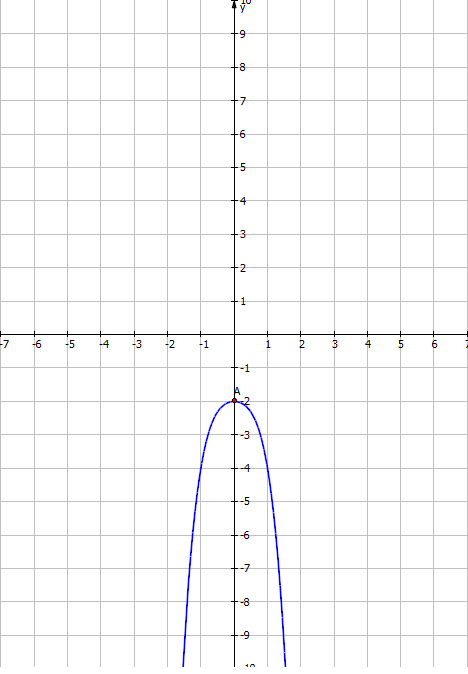
Đồ thị 
Giao với Oy (0;-2)