Bài 14: Viết phương trình đường thẳng trong không gian

I. Lý thuyết
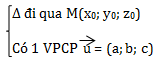\((a^2+b^2+c^2\neq 0)\)
\(pt \ \Delta \left\{\begin{matrix} x=x_0+at\\ y=y_0+bt\\ z=z_0+ct \end {matrix}\right.\)  t tham số 
Nếu a \(\neq\) 0, b \(\neq\) 0, c \(\neq\) 0 thì pt \(\Delta\)

\(\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\) (pt chính tắc)
Chú ý:
1) 
\(\Delta _1 //\Delta 2\)
\(\overrightarrow{u_1}\) là 1 VTCP của \(\Delta _1\)
⇒ \(\overrightarrow{u_1}\) là 1 VTCP của \(\Delta _2\)
2)
 \(\Delta _1\perp \Delta _2\)
\(\overrightarrow{u_1}\) là 1 VTCP của \(\Delta _1\)
\(\overrightarrow{u_2}\) là 1 VTCP của \(\Delta _2\)
ta có \(\overrightarrow{u_1}.\overrightarrow{u_2}=0\)
3) 
\(\left\{\begin{matrix} \overrightarrow{u}\perp \overrightarrow{u_1}\\ \overrightarrow{u}\perp \overrightarrow{u_2} \end{matrix}\right.\) chọn \(\overrightarrow{u}=\left [ \overrightarrow{u_1},\overrightarrow{u_2} \right ]\)
4)
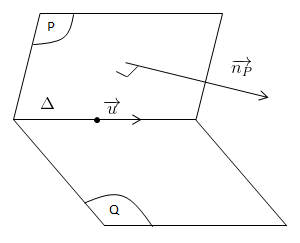
\(\bigg \lbrack \begin{matrix} \Delta \subset (P)\\ \Delta // (P) \end{matrix}\)
\(\overrightarrow{u}\) là 1 VTCP \(\Delta\)
\(\overrightarrow{n_P}\) là VTPT của (P)
Ta có \(\overrightarrow{u}.\overrightarrow{n_P}=0\)
5) 
\(A,B\in \Delta\)
\(\overrightarrow{AB}\) là 1 VTCP của \(\Delta\)
II. Bài tập
VD1: Viết phương trình đường thẳng đi qua 2 điểm A(1;0;3), B(3;2;-1)
Giải
\(\overrightarrow{AB}=(2;2;-4)\)
Đường thẳng \(\Delta\) đi qua  A(1;0;3), nhận \(\overrightarrow{AB}=(2;2;-4)\) hay \(\overrightarrow{u}=(1;1;-2)\) làm 1 VTCP có phương trình
\(\left\{\begin{matrix} x=1+t\\ y=0+t\\ z=3-2t \end{matrix}\right.\)
VD2: Viết phương trình đường thẳng \(\Delta\) đi qua A(1;2;3) đồng thời vuông góc với 2 đường thẳng \(\Delta _1: \frac{x-1}{3}=\frac{y}{1}=\frac{z+1}{2}; \Delta _2:\left\{\begin{matrix} x=-t\\ y=1+2t\\ z=2+3t \end{matrix}\right.\)
Giải
Gọi \(\overrightarrow{u}\) là 1 VTCP của \(\Delta\), ta có:
\(\left\{\begin{matrix} \Delta\perp \Delta_1\\ \Delta\perp \Delta_2 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \overrightarrow{u}\perp \overrightarrow{u_1}=(3;1;2)\\ \overrightarrow{u}\perp \overrightarrow{u_2}=(-1;2;3) \end{matrix}\right.\)
Chọn \(\overrightarrow{u}=\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ] =\left ( \begin{vmatrix} 1 \ 2\\ 2 \ 3 \end{vmatrix}; \begin{vmatrix} 2 \ \ \ \ 3\\ 3 \ -1 \end{vmatrix};\begin{vmatrix} 3 \ \ \ \ 1\\ -1 \ \ 2 \end{vmatrix} \right )=(-1;-11;7)\)
\(pt \ \Delta : \left\{\begin{matrix} x=1-t\\ y=2-11t\\ z=3+7t \end{matrix}\right.\)
VD3: Viết phương trình đường thẳng \(\Delta\) đi qua A(1;2;3) đồng thời vuông góc với \(\Delta _1: \frac{x-1}{2}=\frac{y}{2}=\frac{z+3}{3}\) và song song mặt phẳng \((P):3x-y+2z+1=0\)

Giải
Gọi \(\overrightarrow{u}\) là 1 VTCP của \(\Delta\)
\(\left\{\begin{matrix} \Delta \perp \Delta _1\\ \Delta // P \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \overrightarrow{u}\perp \overrightarrow{u_1}=(2;2;3)\\ \overrightarrow{u}\perp \overrightarrow{u_p}=(3;-1;2) \end{matrix}\right.\)
Chọn \(\overrightarrow{u}=\left [ \overrightarrow{u_1};\overrightarrow{u_P} \right ] =\left ( \begin{vmatrix} 2 \ 3\\ -1 \ 2 \end{vmatrix}; \begin{vmatrix} 3 \ \ 2\\ 2 \ \ 3 \end{vmatrix};\begin{vmatrix} 2 \ \ \ 2\\ 3 \ -1 \end{vmatrix} \right )=(7;5;-8)\)

\(A(1;2;3)\notin (P)\Rightarrow \Delta \not \subset (P)\)
\(pt \ \Delta \left\{\begin{matrix} x=1+7t\\ y=2+5t\\ z=3-8t \end{matrix}\right.\)

VD4: Viết phương trình đường thẳng \(\Delta\) là giao tuyến của hai mặt phẳng (P): \((P): 3x+y+z+2=0 \ (Q): 5x-y+z+4=0\)
Giải
\(M(0;y;z)\in \Delta\)
\(\left\{\begin{matrix} y+z+2=0\\ -y+z+4=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} y=1\\ z=-3 \end{matrix}\right.\Rightarrow M(0;1;-3)\in \Delta\)


Gọi \(\overrightarrow{u}\) là 1 VTCP của \(\Delta\)
\(\left\{\begin{matrix} \Delta \subset (P)\\ \Delta \subset (Q) \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \overrightarrow{u}\perp \overrightarrow{n_P}=(3;1;1)\\ \overrightarrow{u}\perp \overrightarrow{n_Q}=(5;-1;1) \end{matrix}\right.\)

Chọn \(\overrightarrow{u}=\left [ \overrightarrow{u_P};\overrightarrow{u_Q} \right ]= \left ( \begin{vmatrix} 1 \ \ 1\\ -1 \ \ 1 \end{vmatrix};\begin{vmatrix} 1 \ \ \ \ 3\\ 1 \ \ \ \ 5 \end{vmatrix};\begin{vmatrix} 3 \ \ \ \ 1\\ 5 \ -1 \end{vmatrix} \right )=(2;2;-8)\)

\(\overrightarrow{u}'=(1;1;-4)\) là 1 VTCP của \(\Delta\)
\(pt \ \Delta :\left\{\begin{matrix} x=t \ \ \ \ \ \\\ y=1+t \ \ \ \\ z=-3-4t \end{matrix}\right.\)
VD5: Viết phương trình đường thẳng \(\Delta\) đi qua A(-4;-2;4) cắt và vuông góc với đường thẳng \(d\left\{\begin{matrix} x=-3+2t\\ y=1-t \ \ \ \\ z=-1+4t \end{matrix}\right.\)
Giải
\(B=d\cap \Delta\)
\(B=\in d\Rightarrow B(-3+2t;1-t;-1+4t)\)
\(d\perp \Delta \Leftrightarrow \overrightarrow{AB}\perp \overrightarrow{u_d}=(2;-1;4)\)
\(\Leftrightarrow \overrightarrow{AB}\perp \overrightarrow{u_d}=0\)
\(\overrightarrow{AB}=(1+2t;3-t;-5+4t)\)
\(\Leftrightarrow 2(1+2t)-(3-t)+4(-5+4t)=0\)
\(\Leftrightarrow 21t-21=0\Leftrightarrow t=1\)
Vậy B(-1;0;3)
\(\overrightarrow{AB}=(3;2;-1)\)
\(\Delta\) đi qua A(-4;-2;4) và nhận \(\overrightarrow{AB}=(3;2;-1)\) làm 1 VTCP nên có pt
\(\left\{\begin{matrix} x=-4+3t\\ y=-2+2t\\ z=4-t \end{matrix}\right.\)
Nhận xét:
\(\Delta\) đi qua A và cắt d \(\Rightarrow \Delta \subset (A;d)=(Q)\)
\(\Delta\) đi qua A và vuông góc d \(\Rightarrow \Delta \subset (P)\) chứa A và vuông góc d
\(\Delta=(P)\cap (Q)\)