Bài 5: Phương trình logarit - Phương pháp hàm số

I. Lý Thuyết
1)
 \(a>1, y =log_a x\) đồng biến trên \((0;+\infty )\)
\(0<a<1 \ y =log_a x\) nghịch biến trên \((0;+\infty )\)
2) 
+ Tổng 2 hàm số nghịch biến (đồng biến) trên D là hàm số nghịch biến (đồng biến) trên D.
+ Tích 2 hàm số đồng biến, nhận giá trị dương trên D là hàm số đồng biến trên D.
f(x) đồng biến trên D
g(x) nghịch biến trên D
f(x) - g(x) đồng biến trên D
g(x) - f(x) nghịch biến trên D
3) 
f(x) = g(x)
Nếu f(x) đồng biến trên D
g(x) nghịch biến trên D
thì phương trình có tối đa 1 nghiệm.
Khi đó nhẩm nghiệm và chứng minh nghiệm duy nhất.
4)
f(x) = m 
f(x) đồng biến (nghịch biến) trên D
thì phương trình có tối đa 1 nghiệm.
Khi đó nhẩm nghiệm và chứng minh nghiệm duy nhất.

II. Bài tập
VD1: Giải phương trình \(3log_2x+x=10\)
Giải
ĐK: x > 0
x = 4 là 1 nghiệm
x > 4
\(3log_2x>3log_24=6\)
\(\Rightarrow 3log_2x+x>10\)
0 < x < 4
\(3log_2x<6\)
\(\Rightarrow 3log_2x+x< 10\)
Vậy tập nghiệm phương trình là {4}
VD2: Giải phương trình \(2log_5(x+1)+log_7(2x-1)=3\)
Giải

ĐK:
\(\left\{\begin{matrix} x+1>0\\ 2x-1>0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x>-1\\ x>\frac{1}{2} \end{matrix}\right.\Rightarrow x> \frac{1}{2}\)
x = 4 là 1 nghiệm
x > 4
\(2log_5(x+1)>2log_5(4+1)=2\)
\(\Rightarrow log_7(2x-1)>log_7 7=1\)
\(\Rightarrow 2log_5(x+1)+log_7(2x-1)>3\)
\(\frac{1}{2}<x<4\) tương tự \(2log_5(x+1)+log_7(2x-1)<3\)
Vậy tập nghiệm phương trình là {4}
VD3: Giải phương trình \(log_3\frac{x^2+x+3}{2x^2+4x+5}=x^2+3x+2\)
Giải
ĐK: \(\left\{\begin{matrix} \frac{x^2+x+3}{2x^2+4x+5}>0\\ 2x^2+4x+5\neq 0 \end{matrix}\right.\) đúng với mọi x
\(pt\Leftrightarrow log_3(x^2+x+3)-log_3(2x^2+4x+5)=x^2+3x+2\)
Đặt a = x² +x +3, b = 2x² +4x + 5
ta có \(pt\Leftrightarrow log_3a - log_3b=b-a.(*)\)
TH1: a = b thỏa mãn phương trình (*)
\(a=b\Leftrightarrow x^2+x+3=2x^2+4x+5\)
\(\Leftrightarrow x^2+3x+2=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x=-1\\ x=-2 \end{matrix}\)
TH2: a > b
\(\left.\begin{matrix} log_3a -log_3b>0\\ b-a<0 \end{matrix}\right\}VT>0>VP\)
TH3: a < b
tương tự VT < 0 < VP
Vậy tập nghiệm là {-1;-2}
Nhận xét: Có thể trình bày
Cách 2:
\((*)\Leftrightarrow log_3a +a =log_3b+b(**)\)
Xét
 \(f(t)=log_3t +t\)
\(f'(t)=\frac{1}{t ln3}+1> 0 \ \ \ \ \forall t >0\)
\((**)\Leftrightarrow f(a)=f(b)\Leftrightarrow a = b\)
VD4: Giải phương trình 

\(7^{x-1} = 6 log_7(6x-5)+1\)
Giải

ĐK: \(6x-5 > 0\Leftrightarrow x >\frac{5}{6}\)
Đặt \(t-1=log_7(6x-5)\)
\(\Rightarrow 7^{t-1}=6x-5\)
Từ phương trình ta có 
\(7^{x-1}=6(t-1)+1=6t-5\)
\(\Rightarrow 7^{t-1}-6x=7^{x-1}-6t\)
\(\Rightarrow 7^{t-1}+6t=7^{x-1}+6x \ \(1)\)
Xét \(f(y)=7^{y-1}+6y\)
\(f'(y)=7^{y-1}ln7+6>0\)
hàm số đồng biến trên R
\((1)\Leftrightarrow f(t)=f(x)\)
\(\Leftrightarrow t=x\)
\(\Leftrightarrow 7^{x-1}=6x-5\)
\(\Leftrightarrow 7^{x-1}-6(x-1)=1\)
Đặt a = x - 1. ta có 7^a - 6a = 1
Xét \(g(a)=7^a-6a-1\)
\(g'(a)=7^a ln7 -6\)

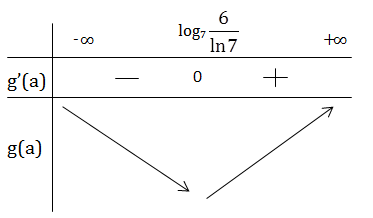
Từ bảng biến thiên ta có phương trình (2) có tối đa 2 nghiệm
a = 0, a = 1 là nghiệm
Tập nghiệm (2) là {0; 1}
\(a=0\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(a=1\Leftrightarrow x-1=1\Leftrightarrow x=2\)
Vậy tập nghiệm phương trình là {1;2}