GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
Bài toán 1: Viết PTTT của đồ thị y = f(x) tại điểm M(x0;y0)
PTTT
|
\(y=f'(x_0).(x-x_0)+y_0\) |
Chú ý: \(y_0=f(x_0)\)
Bài toán 2: Viết PTTT của đồ thị y = f(x) của hệ số góc k
Cách 1: + Gọi hoành độ tiếp điểm là x0
+ Giải phương trình \(f'(x_0)=k\Rightarrow x_0\)
+ Đưa về bt 1
Cách 2: Đường thẳng \(\Delta\) có hệ số góc k thì có pt dạng y = kx + b
\(\Delta\) là tiếp tuyến \(\Leftrightarrow \left\{\begin{matrix} f(x)=kx+b\\ f'(x)=k \ co \ nghiem \end{matrix}\right.\Rightarrow b\Rightarrow \Delta\)
Chú ý:
1) y = f(x) tiếp xúc y = g(x)
Khi hệ \(\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \ co \ nghiem \end{matrix}\right.\)
Bài toán 3: Viết PTTT của đồ thị y = f(x) biết tiếp tuyến đi qua N(x1;y1)
Cách 1:
+ Gọi hoành độ tiếp điểm là x0
+ PTTT: \(y=f'(x_0)(x-x_0)+f(x_0)\)
+ Tiếp điểm đi qua N(x1;y1) nên
\(y_1=f'(x_0)(x_1-x_0)+f(x_0)\Rightarrow x_0\Rightarrow\) đưa về bt 1
Cách 2:
+ Đường thẳng \(\Delta\) đi qua N(x1;y1) có phương trình dạng y = k(x-x1)+y1
+ \(\Delta\) là tiếp tuyến \(\Leftrightarrow \left\{\begin{matrix} f(x)=k(x-x_1)+y_1\\ f'(x)=k \ co \ nghiem \end{matrix}\right.\)\(\Rightarrow k\Rightarrow \Delta\)
Chú ý:
1) \((\Delta _1)y=a_1x+b_1, \ \y=a_2x+b_2\)
\(\Delta _1 // \Delta _2\Leftrightarrow \left\{\begin{matrix} a_1=a_2\\ b_1\neq b_2 \end{matrix}\right.\)
\(\Delta _1 \perp \Delta _2\Leftrightarrow a_1a_2=-1\)
2) Góc giữa 2 đường thẳng \(\begin{matrix} a_1x+b_1y+c_1=0 \ \ \ (\Delta _1)\\ a_2x+b_2y+c_2=0 \ \ \ (\Delta _2) \end{matrix}\)
\(cos(\Delta _1,\Delta _2)=\frac{\left | a_1.a_2+b_1b_2 \right |}{\sqrt{ a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}\)
3) \(M(x_0;y_0) \in\) đồ thị y =f(x)
bt viết phương trình tiếp tuyến tại M
\(\neq\) bt viết phương trình tiếp tuyến tại M
II. Bài tập
VD1: Viết phương trình tiếp tuyến của đồ thị \(y=\frac{x-1}{x+2}\) (C) tại giao điểm của (C) và trục tung.
Giải
Tọa độ giao điểm của (C) và trục tung là nghiệm của hệ
\(\left\{\begin{matrix} x=0\\ y=\frac{x-1}{x+2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=0\\ y=-\frac{1}{2} \end{matrix}\right.\Rightarrow M(0;-\frac{1}{2})\)
\(y'=\frac{x+2-(x-1)}{(x+2)^2}=\frac{3}{(x+2)^2}\)
\(y'(0)=\frac{3}{4}\)
\(y=\frac{3}{4}(x-0)-\frac{1}{2} \ hay \ y=\frac{3}{4}x-\frac{1}{2}\)
VD2: Viết PTTT của đồ thị \(y=\frac{2x+1}{x-2}\). Biết tiếp tuyến đó song song với đường phân giác của góc phần tư thứ hai.
Giải
PT phân giác góc \(\frac{1}{4}\) thứ hai là y = -x
\(\Delta //\Delta _1\) nên có hệ số góc k =-1
\(\Leftrightarrow y'(x_0)=-1\), trong đó x0 là hoành độ tiếp điểm
\(\Leftrightarrow \frac{-5}{(x_0-2)^2}=-1\Leftrightarrow (x_0-2)^2=5\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x_0-2=\sqrt{5}\\ x_0-2=-\sqrt{5} \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix} x_0=2+\sqrt{5}\\ x_0=2-\sqrt{5} \end{matrix}\)
TH1: \(x_0=2+\sqrt{5}\Rightarrow y_0=\frac{5+2\sqrt{5}}{\sqrt{5}}=\sqrt{5}+2\)
PTTT \(y=-1(x-2-\sqrt{5})+2+\sqrt{5}\)
hay \(y=-x+4+2\sqrt{5}\)
TH2: \(x_0=2-\sqrt{5}\Rightarrow y_0=\frac{5-2\sqrt{5}}{-\sqrt{5}}=2-\sqrt{5}\)
PTTT \(y=-(x-2+\sqrt{5})+2-\sqrt{5}\)
hay \(y=-x+4-2\sqrt{5}\)
KL:
\(y=-x+4+2\sqrt{5}\)
\(y=-x+4-2\sqrt{5}\)
Chú ý:
Đường phân giác góc \(\frac{1}{4}\) thứ hai: y = -x
Đường phân giác góc \(\frac{1}{4}\) thứ nhất: y = x
VD3: Viết PTTT của độ thị \(y = x^3-3x^2+2 \ \ \ (C)\) biết tiếp tuyến đi qua điểm M(1;0).
Giải
Gọi hoành độ tiếp điểm là x0
\(y'(x_0)=3x_0^2-6x_0\)
PTTT là tiếp điểm \(y=(3x^2_0-6x_0)(x-x_0)+x_0^3-3x^2_0+2 \ \ (\Delta )\)
\(\begin{matrix} M(1;0)\in \Delta \Leftrightarrow (3x^2_0-6x_0)(1-x_0)+x_0^3-3x^2_0+2 =0 \\ \Leftrightarrow -(3x^2_0-6x_0)(x_0-1)+(x_0-1)(x^2-2x_0-2) =0\ \ \ \ \ \ \ \ \ \ \ \\ \Leftrightarrow (x_0-1)(-2x_0^2+4x_0-2)=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \Leftrightarrow -2(x_0-1)(x_0^2-2x_0+1)=0\Leftrightarrow (x_0-1)^3=0 \Leftrightarrow x_0=1 \end{matrix}\)
PTTT y=-3(x-1)
hay y = -3x +3
VD4: Viết phương trình tiếp tuyến đồ thị \(y=x^3-3x+2\) biết tiếp tuyến đi qua M(2;4).
Giải
+ \(y'=3x^2-3\)
+ Gọi hoành độ tiếp điểm N là x0
Phương trình tiếp tuyến tại tiếp điểm N là
\(y=(3x_0-3)(x-x_0)+x_0^3-3x_0+2\)
- Tiếp tuyến đi qua M(2;4) nên
\((3x_0^2-3)(2-x_0)+x_0^3-3x_0+2=4\)
\(\Leftrightarrow -(3x_0^2-3)(x_0-2)+(x_0-2)(x_0^2+2x_0+1)=0\)
\(\Leftrightarrow (x_0-2)(-2x_0^2+2x_0+4)=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x_0=2\\ -x_0^2+x_0+2=0 \end{matrix}\Leftrightarrow \bigg \lbrack\begin{matrix} x_0=2\\ x_0=-1 \end{matrix}\)
\(x_0=2\) pttt \(y=9(x-2)+4 \ hay \ y=9x-14\)
\(x_0=-1\) pttt \(y=4\)
Vậy có 2 tiếp tuyến y = 4, y = 9x - 14
VD5: Viết phương trình tiếp tuyến của đồ thị \(y=x^4-2x^2+1\) tại điểm cực đại
Giải
\(y'=4x^3-4x\)
\(y'=0\Leftrightarrow 4x(x^2-1)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=1\\ x=-1 \end{matrix}\)
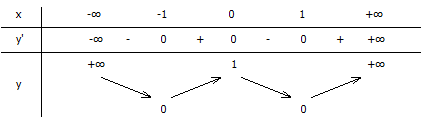
Bt trở thành viết pttt tại điểm K(0;1)
PTTT' \(y=y'(0)(x-0)+1\)
hay y = 1 hay y - 1 = 0














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



