GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
1. Thể tích khối lăng trụ
\(V=S.h\)
S: diện tích đáy
h: chiều cao
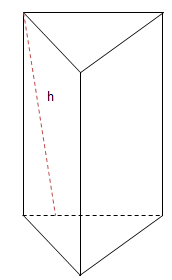
Chú ý:
h = k/c giữa hai đáy
= k/c từ 1 đỉnh thuộc đáy này đến mặt phẳng chứa đáy kia.
1) Thể tích khối hộp chữ nhật có kích thước a, b, c là V = a.b.c
2) Thể tích khối lập phương cạnh a
V = a3
2. Thể tích khối chóp
\(V=\frac{1}{3}.S.h\)
S: diện tích đáy
h: chiều cao (= d (đỉnh; đáy))
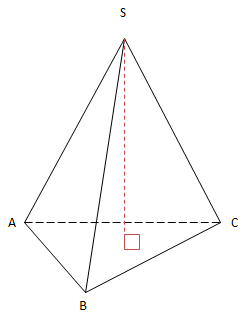
VD1: Cho hình chóp đều S.ABC có SA = a, AB = b. Tính VS.ABC
Giải
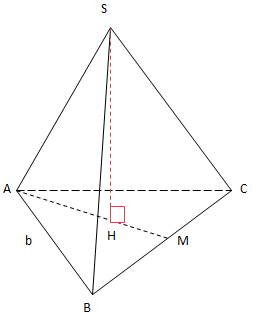
\(\Delta\)ABC đều cạnh AB = b nên
\(S_{ABC}=\frac{b^2.\sqrt{3}}{4}\)
* Kẻ trung tuyến AM
\(M\in BC\)
Gọi H là trọng tâm \(\Delta ABC\) ta có \(SH\perp (ABC). H\in AM\)
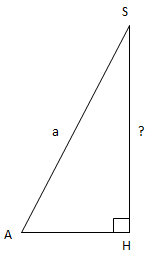
Xét \(\Delta SAH\)
\(AH=\frac{2}{3}AM=\frac{2}{3}.\frac{b\sqrt{3}}{2}=\frac{b\sqrt{3}}{3}\)
Trong \(\Delta SAH\)
\(SH^2=SA^2-AH^2=a^2-\frac{b^2}{3}=\frac{3a^2-b^2}{3}(b< a\sqrt{3})\)
\(V_{S.ABC}=\frac{1}{3}.SH.S_{ABC}=\frac{1}{3}.\frac{\sqrt{3a^2-b^2}}{\sqrt{3}} .\frac{b^2\sqrt{3}}{4}=\frac{1}{12}b^2.\sqrt{3a^2-b^2}\)
Nhận xét:
1) Thể tích khối tự diện đều cạnh a là \(V=\frac{a^3\sqrt{2}}{12}\)
2) Một số bài tập tương tự
Tính thể tích khối chóp đều S.ABC biết AB = b
a) Góc giữa SA và (ABC) là \(\alpha\)
b) Góc giữa (SAB), (ABC) là \(\beta\)
VD2: Cho lăng trụ ABC.A'B'C' có AA'=2a, AB = a, AC = \(a\sqrt{3}, \Delta ABC\) vuông tại A. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm BC. Tính VABC.A'B'C'
Giải
\(\Delta ABC\) vuông tại A nên
\(S_{ABC}=\frac{1}{2}.AB.AC=\frac{1}{2}.a.a\sqrt{3}=\frac{a^2\sqrt{3}}{2}\)
Gọi H là trung điểm BC, ta có \(AH'\perp (ABC)\)
\(\Delta ABC\) vuông tại A nên \(AH=\frac{1}{2}BC\)
\(=\frac{1}{2}.\sqrt{AB^2+AC^2}=a\)
Trong \(\Delta A'HA\), ta có
\(A'H=\sqrt{A'A^2-AH^2}\)
\(=\sqrt{(2a)^2-a^2}=a\sqrt{3}\)
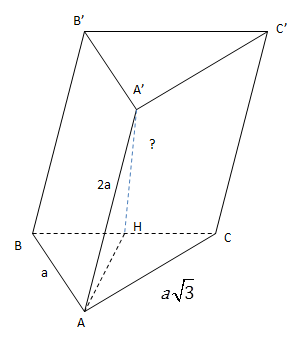
\(V_{ABC.A'B'C'}=A'H.S_{ABC}=a\sqrt{3}.\frac{a^2\sqrt{3}}{2}=\frac{3a^3}{2}\)
VD3: Cho hình chóp tam giác đều cạnh SABC có SA = 2a, AB = a. H là hình chiếu vuông góc của A trên cạnh SC
a) CMR SC \(\perp (ABH)\)
b) Tính VS.ABH
Giải
a,
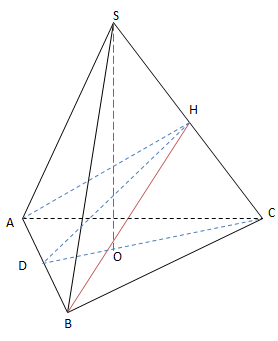
Gọi D là trung điểm AB
O là trọng tâm \(\Delta ABC\)
SC \(\perp\) AH (gt) (1)
\(\left\{\begin{matrix} AB\perp CD \ (\Delta ABC \ deu)\\ AB\perp SO \ (do \ h/c\ SABC \ deu) \end{matrix}\right.\Rightarrow AB\perp (SCD)\)
\(\Rightarrow SC\perp AB \ \ (2)\)
Từ (1) (2) \(SC\perp (ABH)\)
b,
.png)
Tính diện tích \(\Delta\)ABH
HA = HB ( do \(\Delta\)SAC = \(\Delta\) SBC)
\(\Rightarrow HD\perp AB\)
\(SC\perp (ABH)\Rightarrow SC\perp DH\)
DH.SC = SO.DC
\(\Rightarrow DH=\frac{SO.DC}{SC}\)
\(=\frac{\sqrt{SC^2-OC^2}.DC}{SC} \ \ \left ( CD=\frac{a\sqrt{3}}{2}\Rightarrow OC=\frac{2}{3}CD=\frac{a\sqrt{3}}{3} \right )\)
\(=\frac{\sqrt{4a^2-\frac{a^2}{3}}.\frac{a\sqrt{3}}{2}}{2a}= \frac{\frac{a\sqrt{11}}{\sqrt{3}}.\frac{a\sqrt{3}}{2}}{2a}=\frac{a\sqrt{11}}{4}\)
Đường thẳng \(\Delta ABH=\frac{1}{2}.HD.AB=\frac{1}{2}.\frac{a\sqrt{11}}{4}.a=\frac{a^2\sqrt{11}}{8}\)
Trong \(\Delta\)DHC
\(HC=\sqrt{DC^2-DH^2}=\sqrt{\left ( \frac{a\sqrt{3}}{2} \right )^2-\left ( \frac{a\sqrt{11}}{4} \right )^2}\)
\(=\sqrt{\frac{3a^2}{4}-\frac{11a^2}{16}}=\sqrt{\frac{a^2}{16}}=\frac{a}{4}\)
\(SH=SC-HC=2a-\frac{a}{4}=\frac{7a}{4}\)
\(V=\frac{1}{3}.SH.S_{\Delta ABH}=\frac{1}{3}.\frac{7a}{4}.\frac{a^2\sqrt{11}}{8}= \frac{7a^3\sqrt{11}}{96}\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



