Bài 3: Diện tích xung quanh, diện tích toàn phần hình nón

I. Lý thuyết
Cho hình nón có độ dài đường sinh \(\l\), bán kính đáy là R.

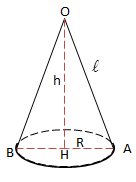
\(S_{xq}=\pi R\l\)
\(S_{tp}=\pi R\l +\pi R^2\)
II. Bài tập
Ví dụ 1: Cho hình nón có độ dài đường sinh là 10cm, độ dài đường cao là 6cm. Tính
a) S_xq
b) S_tp

Giải
Gọi đỉnh h nón là O; tâm đáy là H, A \(\in\) đường tròn đáy
\(OA = 10cm, OH = 6cm\)
Trong tam giác OAH
\(R=HA=\sqrt{OA^2-OH^2}=\sqrt{10^2-6^2}=8(cm)\)
a)
\(S_{xq}=\pi .R.\l =\pi .8.10=80\pi \ (cm^2)\)
b)
\(S_{tp}=\pi .R.\l +\pi R^2 =80\pi+64\pi =144\pi \ (cm^2)\)
Ví dụ 2: Cho hình nón có góc ở đỉnh là 120⁰ độ dài đường sinh là 20(cm). Tính
a) S_xq
b) S_tp

Giải

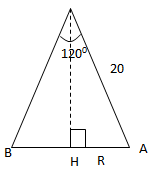
Gọi đỉnh hình nón là O, tâm đáy là H
Kẻ đk của đáy là AB
\(\widehat{AOB}=120^0\Rightarrow \widehat{AOH}=60^0, OA=20\)
Trong tam giác OHA:
\(R=HA=OA.sin\widehat{AOH}=20.sin60^0=20.\frac{\sqrt{3}}{2}=10.\sqrt{3}\)
a)
\(S_{xq}=\pi .R.\l =\pi .10\sqrt{3}.20=200\sqrt{3}\pi \ (cm^2)\)
b)
\(S_{tp}=\pi .R.\l +\pi R^2 =200\sqrt{3}\pi+300\pi =100(2\sqrt{3}+3)\pi \ (cm^2)\)

Ví dụ 3: Cho tam giác ABC vuông tại A, AC = 6 (cm), BC = 10 (cm). Cho đường gấp khúc BAC quay quanh BC, ta được khối tròn xoay. Tính diện tích xung quanh của khối tròn xoay đó.
Giải

 

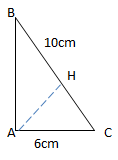
Kẻ AH \(\perp\) BC tại H. Diện tích xung quanh của khối tròn xoay tạo thành chính là tổng diện tích xung quanh của 2 khối nón.
Khối nón thứ nhất được tạo thành khi chop đường gấp khúc BAH quay quanh BH, \(R_1=AH, \l _1=AB\)
\(S_{xp1}=\pi .R^2_1.\l _1=\pi .AH^2.AB\)
Khối nón thứ hai được tạo thành khi cho đường gấp khúc ACH quay quanh CH, \(R_2=AH, \l _2=AC\)
\(S_{xp2}=\pi .R^2_2.\l _2=\pi .AH^2.AB\)

\(S_{xp}=S_{xp1}+S_{xp2}=\pi .AH^2(AB+AC)\)
Trong tam giác ABC. 
\(AB^2=B C^2-AC^2=10^2-6^2=8^2\)
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}= \frac{8^2+6^2}{8^2.6^2}=\frac{5^2}{24^2}\)

\(S_{xq}=\pi .\frac{24^2}{5^2}.(6+8)=\frac{8064}{25}(cm^2)\)