Bài 23: Xác định tọa độ điểm liên quan đến mặt cầu

VD1: Cho mặt cầu (S) \(x^2+y^2+z^2-3x-y+z+\frac{1}{2}=0\). CMR (S) tiếp xúc với (Oyz). Tìm tọa độ tiếp điểm A.
Giải

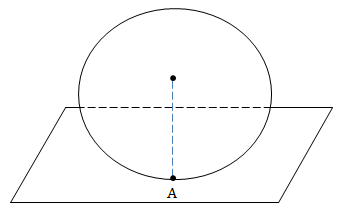
\((S): \left ( x-\frac{3}{2} \right )^2+\left ( y-\frac{1}{2} \right )^2+ \left ( z+\frac{1}{2} \right )^2=\frac{9}{4}\)
(S) có tâm  \(I\left ( \frac{3}{2};\frac{1}{2};-\frac{1}{2} \right ), bk \ R=\frac{3}{2}\)
(Oyz): x = 0 
\(d(I;(oyz))=\frac{\left | \frac{3}{2} \right |}{1}=\frac{3}{2}=R\)
⇒ (oyz) tiếp xúc với (S)
* Tìm tọa độ A

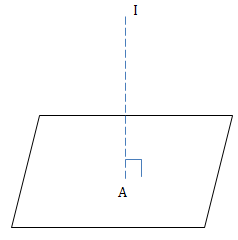
+ Viết phương trình IA: đi qua \(I(\frac{3}{2};\frac{1}{2};-\frac{1}{2})\)
nhận \(\vec{i}=(1;0;0)\) làm VTCP
PT IA: 
\(\left\{\begin{matrix} x=\frac{3}{2}+t\\ y=\frac{1}{2}\\ z=-\frac{1}{2} \end{matrix}\right.\)
\(A=IA\cap (oyz). A\in IA\Rightarrow A(\frac{3}{2}+t;\frac{1}{2};-\frac{1}{2})\)

Vậy \(A(0;\frac{1}{2};-\frac{1}{2})\)
VD2: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) \(x^2+y^2+z^2-2x+4y+2z-3=0\) và \((P): 2x-y+2z-14=0\)
Tìm tọa độ điểm M thuộc (S) sao cho khoảng cách từ M đến (P) lớn nhất, nhỏ nhất.
Giải
\((S): (x-1)^2+(y+2)^2+(z+1)^2=9\)
M \(\in\) (S) nên \((x-1)^2+(y+2)^2+(z+1)^2=9\)
\(d(M;(P))=\frac{\left | 2x-y+2z-14 \right |}{\sqrt{2^2+(-1)^2+2^2}}= \frac{\left | 2x-y+2z-14 \right |}{3}\)
\(=\frac{\left | 2(x-1)-(y+2)+2(z+1)-12 \right |}{3}\)
\(\vec{a}=(x-1;y+2;z+1)\Rightarrow \left | \vec{a} \right |= \sqrt{(x-1)^2+(y+2)^2+(z+1)^2}=3\)
\(\vec{b}=(2;-1;2)\Rightarrow \left | \vec{b} \right |= \sqrt{2^2+(-1)^2+2^2}=3\)
\(-\left | \vec{a} \right |.\left | \vec{b} \right |\leq \vec{a}.\vec{b}\leq \left | \vec{a} \right |.\left | \vec{b} \right |\)
\(\Rightarrow -9\leq 2(x-1)-(y+2)+2(z+1)\leq 9\)
\(\Rightarrow -9\leq 2x-y+2z-2\leq 9\)
\(\Rightarrow -21\leq 2x-y+2z-14\leq -3\)
\(\Rightarrow 3\leq \left | 2x-y+2z-14 \right |\leq 21\)
\(\Rightarrow 1\leq \frac{\left | 2x-y+2z-14 \right |}{3}\leq 7\)
\(\Rightarrow 1\leq d(M;(P))\leq 7\)
GTLN d(M;(P)) = 7 đạt được khi

\(\left\{\begin{matrix} \frac{x-1}{2}=\frac{y+2}{-1}=\frac{z+1}{2}<0\\ 2(x-1)-(y+2)+2(z+1)=-9 \end{matrix}\right.\)
\(\left\{\begin{matrix} x=1+2t\\ y=-2-t\\ z=-1+2t\\ 4t+t+4t=-9 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} t=-1\\ x=-1\\ y=-1\\ z=-3 \end{matrix}\right.\)
Vậy M(-1;-1;-3)
GTNN d(M;(P)) = 1 đạt được khi
\(\left\{\begin{matrix} \frac{x-1}{2}=\frac{y+2}{-1}=\frac{z+1}{2}>0\\ 2(x-1)-(y+2)+2(z+1)=9 \end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} t=1\\ x=3\\ y=-3\\ z=1 \end{matrix}\right.\Rightarrow M(3;-3;1)\)
VD3: Tìm tọa độ điểm M thuộc mặt cầu \((S): x^2+y^2+z^2-2x-4y+2z-3=0\). Sao cho độ dài MA lớn nhất, nhỏ nhất, trong đó A(1;-2;0)
Giải
\((S): (x-1)^2+(y-2)^2+(z+1)^2=9\)
Xét mp (P) chứa IA
(P) cắt (S) theo đường tròn 
bán kính R=3, gọi đường tròn là (C)
\(IA\cap (C)=\left \{ M_1,M_2 \right \} \ (AM_1<AM_2)\)
Ta chứng minh AM₁ = min AM   M \(\in\)
(S)
Xét M bất kì \(\in\) (S)
Ta có
\(AM+MM_2\geq AM_2=AM_1+M_1M_2\)
Lại có \(MM_2\leq M_1M_2=2R\)
Suy ra \(AM\geq AM_1\)
GTNN \(AM=AM_1 \ khi \ M\equiv M_1\)
Tương tự 
GTLN \(AM=AM_2 \ khi \ M\equiv M_2\)
\(\left \{ M_1,M_2 \right \}=IA\cap (S)\)
(S) có tâm I(1;2;-1)
\(\overrightarrow{IA}=(0;-4;1)\)
Phương trình IA
\(\left\{\begin{matrix} x=1\\ y=-2-4t\\ z=t \end{matrix}\right.\)
\(M\in IA\Rightarrow M(1;-2-4t;t)\)
\(M\in (S)\Leftrightarrow (1-1)^2+(-4-4t)^2+(t+1)^2=9\)
\(\Leftrightarrow 17t^2+34t+17=9\)
\(\Leftrightarrow 17t^2+34t+8=0\)
\(\Delta '=17^2-17.8=17.9, \sqrt{\Delta '}=3\sqrt{17}\)
\(\Bigg \lbrack\begin{matrix} t=\frac{-17-3\sqrt{17}}{17 }\Rightarrow M_2(1;\frac{34+12\sqrt{17}}{17};\frac{-17-3\sqrt{17}}{17})\\ \\ t=\frac{-17+3\sqrt{17}}{17}\Rightarrow M _1(1;\frac{34-12\sqrt{17}}{17};\frac{-17+3\sqrt{17}}{17}) \end{matrix}\)
Vậy AM nhỏ nhất khi 
\(M(1;\frac{34-12\sqrt{17}}{17};\frac{-17+3\sqrt{17}}{17})\)
AM lớn nhất khi 
\(M(1;\frac{34+12\sqrt{17}}{17};\frac{-17-3\sqrt{17}}{17})\)