Bài 3: Ứng dụng của tích vô hướng chứng minh quan hệ vuông góc, tính góc

I. Lý thuyết
\(\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.cos(\vec{a},\vec{b})\)
\(\left.\begin{matrix} \vec{a}=(x_1;y_1;z_1)\\ \vec{b}=(x_2;y_2;z_2) \end{matrix}\right\} \vec{a}.\vec{b} = x_1.x_2 + y_1.y_2 + z_1.z_2\)
\(cos(\vec{a};\vec{b})=90^0\Leftrightarrow x_1.x_2+y_1.y_2+z_1.z_2=0\)
II. Bài tập
VD1: Cho S(2;2;6), A(4;0;0), B(4;4;0), C(0;4;0), O(0;0;0). CRM: S.ABCO là hình chóp tứ giác đều.
Giải
Chứng minh ABCO là hình vuông
\(\overrightarrow{OA}=(4;0;0)\)
\(\overrightarrow{CB}=(4;0;0)\)
\(\overrightarrow{OA}=\overrightarrow{CB}\Rightarrow ABCO\) là hình bình hàng (1)


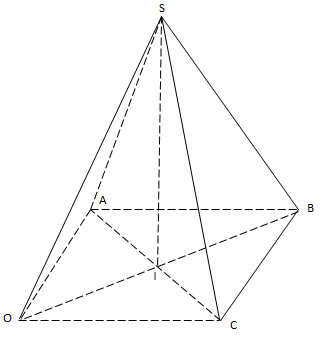
\(\overrightarrow{AB}=(0;4;0)\Rightarrow AB=4=OA \ \ (2)\)
\(\overrightarrow{OA}.\overrightarrow{AB}=4.0+0.4+0.0=0\Rightarrow OA\perp AB \ \ (3)\)
Từ (1) (2) (3) ta có ABCO là hình vuông
I là trung điểm AC \(\Rightarrow I(2;2;0)\) là tâm hình vuông
\(\overrightarrow{SI}=(0;0;-6)\)
\(\overrightarrow{SI}.\overrightarrow{OA}=0.4+0.0+0.(-6)=0\Rightarrow SI\perp OA\)
\(\overrightarrow{SI}.\overrightarrow{AB}=0.0+0.4+(-6).0=0\Rightarrow SI\perp AB\)
\(\Rightarrow SI\perp (OAB)\)
Vậy S.ABCO là hình chiếu tứ giác đều
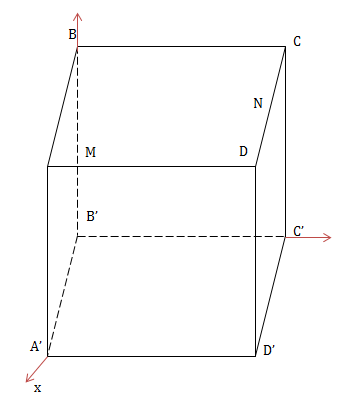
VD2: Cho hình lập phương ABCD.A'B'C'D' cạnh a. M, N lần lượt là trung điểm BB',A'D'. CRM: \(MN\perp AC'\)
Giải
Chọn hệ trục tọa độ
Để các vuông góc
B'xyz \(B'x\equiv B'A'\)
\(B'y\equiv B'C',B'Z\equiv B'B\)
B'(0;0;0)
B(0;0;a)
A'(a;0;0)  A(a;0;a)
D'(a;a;0)  D(a;a;a)
C'(0;a;0)  C(0;a;a)
M là trung điểm BB' nên \(M(0;0;\frac{a}{2})\)
N là trung điểm A'D' nên \(N(a;\frac{a}{2};0)\)
\(\overrightarrow{MN}=(a;\frac{a}{2};-\frac{a}{2})\)
\(\overrightarrow{AC'}=(-a;a;-a)\)
\(\overrightarrow{MN}.\overrightarrow{AC'}=a.(-a)+\frac{a}{2}.a+(-\frac{a}{2})(-a)=0\)

Vậy \(MN\perp AC'\)
VD3: Trong không gian với hệ tọa độ Oxyz cho hình chóp S.ABCD có đáy là hình thoi. AC cắt BD tại gốc tọa độ A(2;0;0), B(0;1;0), S(0;0;\(2\sqrt{2}\)). M là trung điểm SC. Tính góc giữa SA và MB.
Giải
O là trung điểm AC
\(\left\{\begin{matrix} x_c=2x_0-x_A=-2\\ y_c=2y_0-y_A=0\\ z_c=2z_0-z_A=0 \end{matrix}\right.\Rightarrow C(-2;0;0)\)
M là trung điểm SC nên M(-1;0; \(\sqrt{2}\))
\(\overrightarrow{MB}=(1;1;-\sqrt{2})\)
\(\overrightarrow{SA}=(2;0;-2\sqrt{2})\)
\(cos(SA;MB)=\left | cos(\overrightarrow{SA};\overrightarrow{MB}) \right |\)
\(=\frac{\left | 2+1.0+(-\sqrt{2})(-2\sqrt{2}) \right | }{ \sqrt{ 1^2+1^2+(-\sqrt{2})^2}.\sqrt{2^2+0^2+(-2\sqrt{2})^2}}\)
\(=\frac{6}{2.2\sqrt{3}}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow (\widehat{SA, MB})=30^0\)
Chú ý:
\(coss(SA;MB)=\left | cos(\overrightarrow{SA};\overrightarrow{MB}) \right | =\frac{\left | \overrightarrow{SA}.\overrightarrow{MB} \right |}{SA.MB}\)