Bài 7: Bài toán tìm cực trị

1. Lý thuyết

a)
- Hàm số f(x) đạt cực đại tại x₀ nếu \(f(x_0)>f(x) \ \forall x\in (x_0-h,x_0+h) \setminus \left \{ x_0 \right \},h>0\)

- Hàm số f(x) đạt cực tiểu tại x₀ nếu \(f(x_0)0\)

b) ĐK cần để hàm số đạt cực trị

+ f(x) đạt cực trị tại x₀, có đạo hàm tại x₀ thì f(x₀) = 0

c) ĐK đủ để hàm số đạt cực trị

\(x_0\in (a;b)\) f(x) có đạo hàm trong (a;b) (có thể tìm x₀)

- Điều kiện thứ nhất: Tính từ trái sang phải

+ Nếu f(x) đã đổi dấu từ + sang - khi qua x₀ thi x₀ là cực đại

+ Nếu f(x) đã đổi dấu từ - sang + khi qua x₀ thi x₀ là cực tiểu

- Điều kiện thứ hai: f(x) có đạo hàm đến cấp hai trong (a;b), \(x_0\in (a;b),A\Rightarrow f'(x_0)=0\)

+ Nếu f''(x0) > 0 thì x₀ là cực tiểu

+ Nếu f''(x0) < 0 thì x₀ là cực đại

2. Bài tập

VD1: Tìm cực trị của hàm số \(f(x)=x^3-3x^2\)
Giải
TXĐ: R
\(f'(x)=3x^2-6x\)
\(f'(x)=0\Leftrightarrow 3x(x-2)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=2 \end{matrix}\)

 

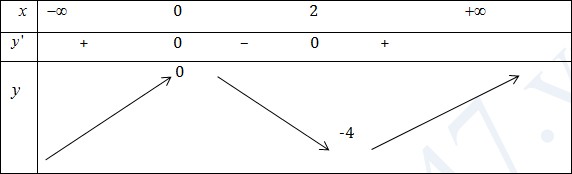
Hàm số đại cực đại tại x_CĐ = 0, y_CĐ = 0

Hàm số đại cực đại tiểu x_CT = 2, y_CT = -4

Chú ý: Các bước trên cực trị

+ TXĐ

+ Tính f’(x), giải phương trình f’(x) = 0

+ Lập bảng biên thiên  => KL

+ Tính giá trị f’’(x), xét dấu f’’(x _{tới hạn})
VD2: Tìm cực trị của hàm số \(f(x)=x^3+3x^2+3x+2\)
Giải
TXĐ: R
\(f'(x)=3x^2+6x+3=3(x^2+2x+1)=3(x+1)^2\)
\(f'(x)=0\Leftrightarrow x=-1\)

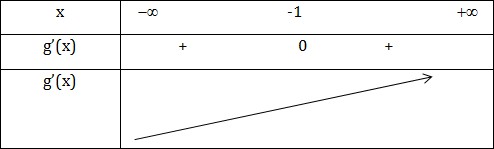
Hàm số không có cực trị
VD3: Tìm cực trị của hàm số \(f(x)=\left | x-1 \right |\)
Giải
\(f(x)=\left\{\begin{matrix} x-1 \ \ neu \ \ x\geq 1\\ -x+1 \ \ neu \ \ x<1 \end{matrix}\right.\)
\(f'(x)=\left\{\begin{matrix} 1 \ \ neu \ \ x>1\\ -1 \ \ neu \ \ x<1 \end{matrix}\right.\)

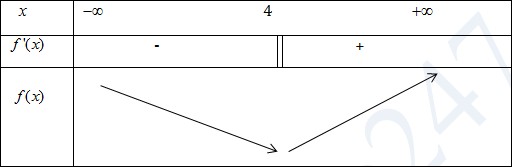
Hàm số đạt cực tiểu tại x_ct = 1 ⟹ y_ct = 0
Chú ý: 
1) Hàm số đạt cực trị tại x₀ thì \(\bigg \lbrack\begin{matrix} f'(x_0)=0 \\ f'(x) \ \ k^0 xac \ dinh \ tai \ x_0 \end{matrix}\)
2) Hàm số f(x) không có đạo hàm tại x₀ thị vẫn có thể đạt cực trị tại x0
3) \(f(x)=\left | x-1 \right |=\sqrt{(x-1)^2}\)
\(f'(x)=\frac{2(x-1)}{2\sqrt{(x-1)^2}}=\frac{x-1}{\left | x-1 \right |} = \left\{\begin{matrix} 1 \ \ x>1\\ -1 \ \ x<1 \end{matrix}\right.\)
VD4: Tìm cực trị của hàm số \(f(x)=\frac{x^2+2x+2}{x+1}\)
Giải
TXĐ:  D = R\{1}
\(f'(x)=\frac{(2x+1)(x+1)-(x^2+2x+2)}{(x+1)^2}=\frac{x^2+2x}{(x+1)^2}\)
\(f'(x)=0\Leftrightarrow x^2+2x=0\Leftrightarrow \begin{bmatrix} x=0\\ x=-2 \end{matrix}\)

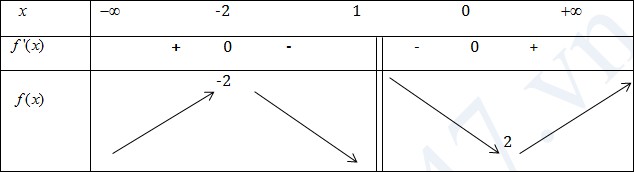
Hàm số đạt cực đại tại x_CĐ = -2, y_CĐ = -2
Hàm số đạt cực tiểu tại x_CT = 0, y_CT = 2
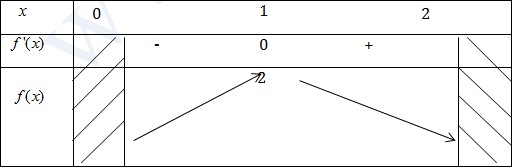
VD5: Tìm cực trị của hàm số \(f(x)=\sqrt{x}+\sqrt{2-x}\) 
Giải
TXĐ: [0;2]
\(f'(x)=\frac{1}{2\sqrt{x}}-\frac{1}{2\sqrt{2-x}}\)
\(f'(x)=0\Leftrightarrow \sqrt{x}=\sqrt{2-x}\)
\(\Leftrightarrow x=2-x\Leftrightarrow x=1\)

 

VD6: Tìm cực trị của hàm số \(f(x)=sin^2x-\sqrt{3}cosx\) trên \([0;\pi]\)
Giải
\(f'(x)=2.(sinx)'.sinx-\sqrt{3}(cosx)'=2.cosx.sinx+\sqrt{3}sinx\)
\(=sinx(2cosx+\sqrt{3})\)
\(f'(x)=0\Leftrightarrow \bigg \lbrack\begin{matrix} sinx=0\\ cosx=-\frac{\sqrt{3}}{2} \end{matrix}\) do \(x\in [0;\pi]\)
\(\Bigg \lbrack\begin{matrix} x=0\\ x=\pi\\ x=\frac{5\pi}{6} \end{matrix}\)
\(f''(x)=2.cos2x+\sqrt{3}cosx\)
\(f''(0)=2+\sqrt{3}>0, \ x_{CT}=0, y_{CT}=-\sqrt{3}\)
\(f''(\pi)=2-\sqrt{3}>0, \ x_{CT}=\pi, y_{CT}=\sqrt{3}\)
\(f''(\frac{5\pi}{6})=1-\frac{3}{2}=-\frac{1}{2}<0, \ x_{CD}=\frac{5\pi}{6}, y_{CD}=\frac{7}{4}\)