Bài 1: Tìm khoảng đơn điệu của hàm số

Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm khoảng đơn điệu của hàm số như:

• Định nghĩa
• Điều kiện đủ để hàm số đơn điệu
• Các bước tìm khoảng đơn điệu của hàm số

1. Định nghĩa
Cho hàm số f(x) xác định trên (a;b)
a) f(x) đồng biến trên (a;b) nếu
\(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)<f(x_2)\)
b) f(x) nghịch biến trên (a;b) nếu
\(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)>f(x_2)\)
2. Điều kiện đủ để hàm số đơn điệu
Cho hàm số f(x) xác định và liên tục trên (a;b)
a) Nếu \(f'(x) >0 \forall x\in (a;b)\) thì f(x) đồng biến trên (a;b)
Nếu \(f'(x) <0 \forall x\in (a;b)\) thì f(x) thì nghịch biến trên (a;b)
b) Nếu \(f'(x)\geq 0\forall x\in (a;b)\) và f'(x) = 0 tại hữu hạn điểm thuộc (a;b) thì f(x) đồng biến trên (a;b)
Nếu \(f'(x) \leqslant 0\forall x\in (a;b)\) và f'(x) = 0 tại hữu hạn điểm thuộc (a;b) thì f(x) nghịch biến trên (a;b)
3. Tìm khoảng đơn điệu của hàm số
B1: Tìm TXĐ
B2: Tính f'(x)
Tìm nghiệm f'(x) = 0
B3: Dựa vào định lý ⇒ KL (Bảng biến thiên)
Chú ý: 
1) Dấu của f(x) = ax + b (\(a\neq 0\))

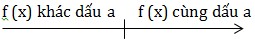
2) Dấu của f(x) = ax² + bx + c (\(a\neq 0\))
\(\Delta <0\) thì f(x) cùng dấu a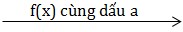  
\(\Delta =0\) thì f(x) cùng dấu với a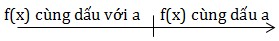 
\(\forall x\neq -\frac{b}{2a}(f(-\frac{b}{2a})=0)\)
\(\Delta >0\) thì f(x) = 0 có 2 nghiệm \(x_1.x_2(x_1<x_2)\)

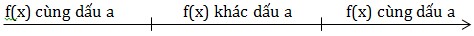
Quy tắc:  “Ngoài cùng trong khác”
VD1: Tìm khoảng đơn điệu của hàm số \(f(x)=-x^3+3x^2\)
Giải
TXĐ: D = R
\(f'(x)=-3x^2+3.2x\)
\(=-3x(x-2)\)
\(f'(x)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=2 \end{matrix}\)

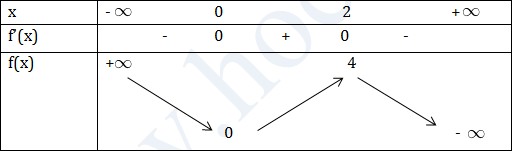
Hàm số đồng biến trên (0;2) 
Hàm số nghịch biến trên các khoảng \((-\infty ;0);(2;+\infty)\)

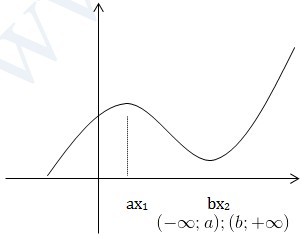
Chú ý: Hàm số đồng biến nghịch biến trên (a;b); (c;d) thì chưa chắc đồng biến (nghịch biến) ​trên \((a;b)\cup (c;d)\)
VD2: Tìm khoảng đơn điệu của hàm số \(f(x)=x^3-3x^2+3x+2\)
Giải 
TXĐ: D = R
\(f'(x)=3x^2-6x+3\)
\(=3(x^2-2x+1)\)
\(=3(x-1)2\)
\(f'(x)\geq 0 \ \forall x, f'(x)=0\Leftrightarrow (x-1)^2=0\Leftrightarrow x=1\)

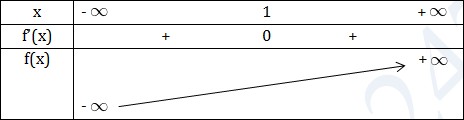
Hàm số đồn biến trên R
VD3: Tìm khoảng đơn điệu của hàm số \(f(x)=x^3+x^2+8x+6\)
Giải
TXĐ: D = R
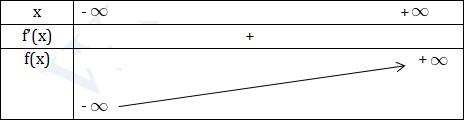
\(f'(x)=3x^2+2x+8>0 \ \forall x\in R\)
Vì \(\left\{\begin{matrix} \Delta '=1-3.8=-23< 0\\ a=3>0 \end{matrix}\right.\)
Kết luận: Hàm số đồng biến trên R

VD4: Tìm khoảng đơn điệu của hàm số \(f(x)=x^4-2x^2\)
Giải
TXĐ: D = R
\(f'(x)=4x^3-4x\)
\(=4x(x^2-1)\)
\(f'(x)=0\Leftrightarrow 4x(x^2-1)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=1\\ x=-1 \end{matrix}\)

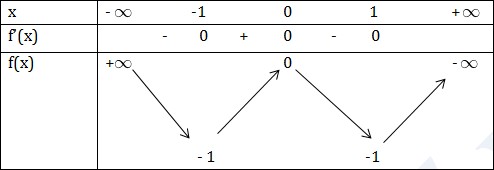
KL: Hàm số đồng biến trên \((-1;0);(1;+\infty )\)
Hàm số nghịch biến trên \((-\infty ;-1);(0;1 )\)
VD5: Tìm khoảng đơn điệu của hàm số \(f(x)=\frac{8x+6}{2x-3}\)
Giải
TXĐ: \(D = R \setminus\left \{ \frac{3}{2} \right \}\)
\(f'(x)=\frac{8(2x-3)-2(8x+6)}{(2x-3)^2}=\frac{-36}{(2x-3)^2}< 0\)

KL: Hàm số nghịch biến \((-\infty ;\frac{3}{2}); (\frac{3}{2};+\infty )\)
VD6: Tìm khoảng đơn điệu của hàm số \(f(x)=\sqrt{x-2}+\sqrt{4-x}\)
Giải
TXĐ: Hàm số xác định khi \(\left\{\begin{matrix} x-2\geqslant 0\\ 4-x\geq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geqslant 2\\ x\leqslant 4 \end{matrix}\right.\)
D=[2;4]
\(f'(x)=\frac{1}{2\sqrt{x-2}}-\frac{1}{2\sqrt{4-x}}\)
\(f(x)=0\Rightarrow \sqrt{x-2}=\sqrt{4-x}\)
\(\Rightarrow x-2=4-x\)
\(\Rightarrow x=3\in [2;4]\)

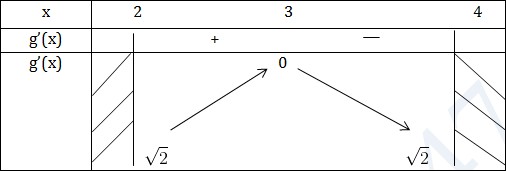
Hàm số nghịch biến trên (3;4)
Hàm số đồng biến trên  (2;3)