Bài 16: Khoảng cách giữa hai đường thẳng, đường thẳng và mặt phẳng song song

I. Lý thuyết
1. Khoảng cách từ 1 điểm đến đường thẳng
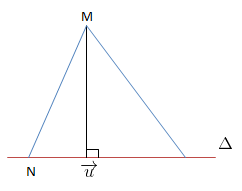
Cho điểm M và đường thẳng $\Delta$ đi qua N và có 1 VTCP $\overrightarrow{u}$
$d(M;\Delta )=\frac{\left | \left [ \overrightarrow{NM};\overrightarrow{u} \right ] \right |}{\left | \overrightarrow{u} \right |}$
$\left ( =\frac{2S_{\Delta MNP}}{NP} \right )$ 

2) Khoảng cách từ giữa đường thẳng và mặt phẳng song song 

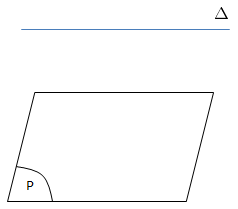
Cho đường thẳng $\Delta$ và mặt phẳng (P), $\Delta$ // (P) Ax+By+Cz+D=0, M(x₀;y₀;z₀)
$d(\Delta;(P))=d(M;(P)) \ \ M \in \Delta$
$=\frac{\left | Ax+By+Cz+D \right |}{\sqrt{A^2+B^2+C^2}}$

3) Khoảng cách giữa hai đường thẳng chéo nhau
Cách 1:
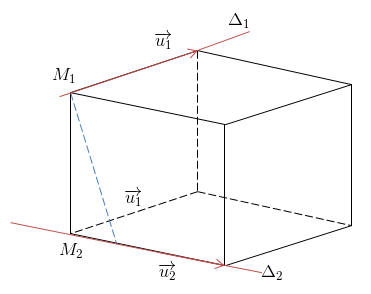
$\Delta _1$ đi qua M₁. có 1 VTCP $\overrightarrow{u_1}$
$\Delta _2$ đi qua M₂. có 1 VTCP $\overrightarrow{u_2}$
$d(\Delta _1;\Delta _2)=\frac{\left | [\overrightarrow{u_1};\overrightarrow{u_2}] .\overrightarrow{M_1M_2}\right |}{[\overrightarrow{u_1};\overrightarrow{u_2}]}$
 

Cách 2:
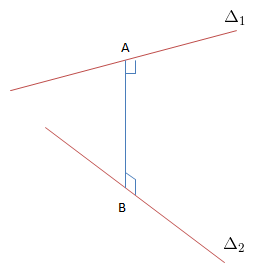
AB là đoạn vuông góc chung $\Delta _1$, $\Delta _2$
$A\in \Delta _1, B\in \Delta _2$
$\Leftrightarrow \left\{\begin{matrix} \overrightarrow{AB}.\overrightarrow{u_1}=0\\ \overrightarrow{AB}.\overrightarrow{u_2}=0 \end{matrix}\right.$
$d(\Delta _1;\Delta _2)=AB$

II. Bài tập

VD1: Cho điểm M(1;2;3) và $\Delta :\frac{x-1}{2}=\frac{y}{2}=\frac{z+1}{1}$. Tính $d(M;\Delta )$
Giải
$\Delta$ đi qua N(1;0;-1) và có 1 VTCP $\overrightarrow{u}=(2;2;1)$
$d(M;\Delta )=\frac{\left | [\overrightarrow{NM};\overrightarrow{u}] \right |}{ \left | \overrightarrow{u} \right |}$
$\left.\begin{matrix} \overrightarrow{NM}=(0;2;4)\\ \overrightarrow{u}=(2;2;1) \end{matrix}\right\}$
$[\overrightarrow{NM};\overrightarrow{u}] = \left ( \begin{vmatrix} 2 \ \ 4 \\ 2 \ \ 1 \end{vmatrix}; \begin{vmatrix} 4 \ \ 0 \\ 1 \ \ 2 \end{vmatrix}; \begin{vmatrix} 0 \ \ 2 \\ 2 \ \ 2 \end{vmatrix} \right )=(-6;8;-4)$
$d(M;\Delta )=\frac{\left | [\overrightarrow{NM};\overrightarrow{u}] \right |}{ \left | \overrightarrow{u} \right |}= \frac{\sqrt{(-6)^2+8^2+(-4)^2}}{\sqrt{2^2+2^2+1^2}}=\frac{\sqrt{116}}{3} =\frac{2.\sqrt{29}}{3}$
Cách 2:

$H\in \Delta \Rightarrow H(1+2t;2t;-1+t)$
$\overrightarrow{MH}=(2t;2t-2;-4+t)$
H là hình chiếu M trên $\Delta$ nên 
$\overrightarrow{MH}.\overrightarrow{u}=0\Leftrightarrow 4t+2(2t-2)-4+t=0$
$\Leftrightarrow 9t=8\Leftrightarrow t=\frac{8}{9}$
$\overrightarrow{MH}=(\frac{16}{9};-\frac{2}{9};-\frac{28}{9})$
$d(M;\Delta )=MH=\frac{\sqrt{16^2+(-2)^2+(-28)^2}}{9}=\frac{2\sqrt{29}}{3}$
Nhận xét:
1) Tìm $H\in \Delta$ sao cho MH_min

VD2: Tìm tọa độ điểm N thuộc đường thẳng $\Delta: \frac{x}{2}=\frac{y}{3}=\frac{z-1}{1}$ và cách d $\left\{\begin{matrix} x=-1-t\\ y=3+2t\\ z=4+3t \end{matrix}\right.$ một khoảng bằng $\frac{13\sqrt{42}}{14}$.
Giải
$N\in \Delta \Rightarrow N(2t;3t;1+t)$
d đi qua M(-1;3;4), có 1 VTCP $\overrightarrow{u}=(-1;2;3)$
$\overrightarrow{MN}=(2t+1;3t-3;t-3)$
$\overrightarrow{u}=(-1;2;3)$
$\left [ \overrightarrow{MN};\overrightarrow{u} \right ]= \left ( \begin{vmatrix} 3t-3 \ \ t-3\\ 2 \ \ \ \ \ \ \ \ \ 3 \end{vmatrix}; \begin{vmatrix} t-3 \ \ 2t+1\\ 3 \ \ \ \ \ \ \ \ \ -1 \end{vmatrix}; \begin{vmatrix} 2t+1 \ \3t-3\\ -1 \ \ \ \ \ \ \ \ \ 2 \end{vmatrix} \right )$
$= (7t-3;-7t;7t-1)$
$d(N;d)=\frac{\left | [\overrightarrow{MN};\overrightarrow{u}] \right |}{\left | \overrightarrow{u} \right |}=\frac{\sqrt{(7t-3)^2+(-7t)^2+(7t-1)^2}}{\sqrt{(-1)^2+2^2+3^2}}$
$=\frac{\sqrt{147t^2-56t+10}}{\sqrt{14}}$
$d(N;d)=\frac{13\sqrt{42}}{14}$
$\Leftrightarrow \frac{147t^2-56t+10}{14}=\frac{169.42}{14^2}$
$\Leftrightarrow 147t^2-56t-497=0$
$\Leftrightarrow \Bigg \lbrack\begin{matrix} t=\frac{28-\sqrt{73843}}{147}\\ \\ t=\frac{28+\sqrt{73843}}{147} \end{matrix}$
$\Rightarrow N\left ( \frac{56\mp 2\sqrt{73843}}{147}; \frac{84\mp 3\sqrt{73843}}{147} ; \frac{175\mp 2\sqrt{73843}}{147} \right )$

VD3: Cho đường thẳng $\Delta \frac{x+1}{-1}=\frac{y-2}{2}=\frac{z}{3}$ và $(P):2x+y+mz-1=0$
a) Tìm m để $\Delta //(P)$
b) Tính $d(\Delta ;(P))$
Giải
$\Delta$ đi qua M(-1;2;0), có 1 VTCP $\overrightarrow{u}=(-1;2;3)$
(P) có 1 VTPT $\overrightarrow{n_P}=(2;1;m)$
a)
$\Delta$ // (P) $\Leftrightarrow\left\{\begin{matrix} M\notin (P)\\ \overrightarrow{u}.\overrightarrow{n_P}=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -2+2+0-1\neq 0\\ -2+2+3m=0 \end{matrix}\right.\Leftrightarrow m=0$
b)
Với m = 0
$(P): 2x+y-1=0$
$d(\Delta ;(P))=d(M;(P))=\frac{\left | -2+2-1 \right |}{\sqrt{2^2+1^2}}=\frac{1}{\sqrt{5}}$
VD4: Cho $(d_1)\left\{\begin{matrix} x=1+2t\\ y=2+t\\ z=-3+3t \end{matrix}\right.(d_2)\left\{\begin{matrix} x=2+u\\ y=-3+2u\\ z=1+3u \end{matrix}\right.$
a) CMR: d₁, d₂ chéo nhau
b) Tính d(d₁;d₂)
Giải
a)
d₁ đi qua M₁(1;2;-3), có 1 VTCP $\overrightarrow{u_1}=(2;1;3)$
d₂ đi qua M₂(2;-3;1), có 1 VTCP $\overrightarrow{u_2}=(1;2;3)$
$\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]= \left ( \begin{vmatrix} 1 \ \ 3\\ 2 \ \ 3 \end{vmatrix};\begin{vmatrix} 3 \ \ 2\\ 3 \ \ 1 \end{vmatrix};\begin{vmatrix} 2 \ \ 1\\ 1 \ \ 2 \end{vmatrix} \right )=(-3;-3;3)$
$\overrightarrow{M_1M_2}=(1;-5;4)$
$\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ].\overrightarrow{M_1M_2}= -3.1+(-3)(-5)+3.4=24\neq 0$
Vậy d₁, d₂ chéo nhau
b)
Cách 1:
$d(d_1;d_2)=\frac{\left | [\overrightarrow{u_1};\overrightarrow{u_2}.\overrightarrow{M_1M_2 }] \right |}{\left | \overrightarrow{u_1};\overrightarrow{u_2} \right |}= \frac{24}{\sqrt{(-3)^2+(-3)^2+3^2}}=\frac{24}{3\sqrt{3}}=\frac{8}{\sqrt{3}}$
$=\frac{8\sqrt{3}}{3}$
Cách 2: 
$A(1+2t;2+t;-3+3t)\in d_1$
$B(2+u;-3+2u;1+3u)\in d_2$
AB là đoạn vuông góc chung
$\Leftrightarrow \left\{\begin{matrix} \overrightarrow{AB}.\overrightarrow{u_1}=0\\ \overrightarrow{AB}.\overrightarrow{u_2}=0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} t\\ u \end{matrix}\right.$
AB = d(d₁;d₂)