Bài 3: Tính thể tích bằng cách gián tiếp

I. Lý thuyết

1. Nếu hai khối có cùng chiều cao thì $\frac{V_1}{V_2}=\frac{S_1}{S_2}$

2. Nếu hai khối chóp có cùng diện tích đáy

$\frac{V_1}{V_2}=\frac{h_1}{h_2}$

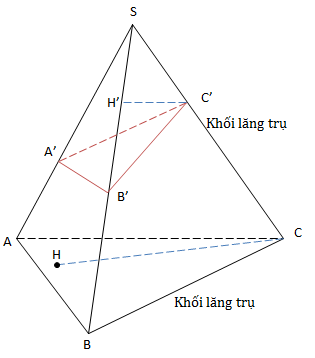
3. Cho hình chóp S.ABC, $A'\in SA, B'\in SB, C'\in SC$. 

$\frac{V_{SA'B'C'}}{V_{SABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}$

Chứng minh:
$\frac{V_{SA'B'C'}}{V_{SABC}}=\frac{V_{C'.SA'B'}}{V_{C.SAB}}= \frac{\frac{1}{3}.C'H'.dt \ \Delta SA'B'}{\frac{1}{3}CH.dt \ \Delta SAB}= \frac{SC'}{SC}.\frac{SA'}{SA}.\frac{SB'}{SB}$

II. Bài tập
VD1: Cho hình chóp S.ABC, d(SA, BC) = d, góc giữa SA và BC bằng $\alpha$. CMR: $V_{SABC}=\frac{1}{6}SA.BC.d.sin\alpha$
Giải
Dựng hình bình hành ABCD
AD // BC, AD = BC
$sin\widehat{(SA;BC)}=sin\alpha =sin\widehat{SAD}$

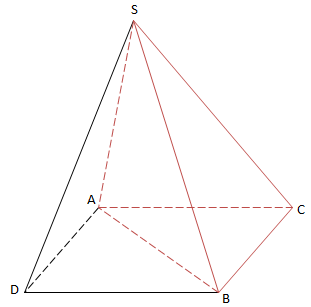
d = k/c (BC;(SAD)) do BC // AD

   = d(B;(SAD))

$dt \ \Delta ABC=dt \ \Delta ABD$

$V_{S.ABC}=V_{SABD}=V_{B.SAD}=\frac{1}{3}.d(B;(SAD)).dt \ \Delta SAD$

$=\frac{1}{3}.d.\frac{1}{2}.SA.AD.sin\widehat{SAD}$

$=\frac{1}{6}.d.SA.AD.sin\alpha =\frac{1}{6}d.SA.BC.sin\alpha$

VD2: Tính thể tích của khối tứ diện ABCD biết AB = CD = a, AD = BC = b, AC = BD = c.
Giải

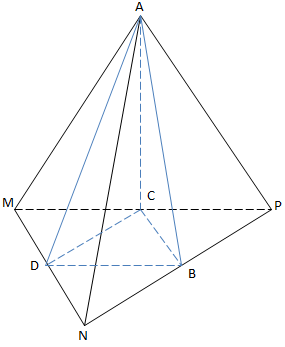
Cách 1
Gọi M, N, P là các điểm sao cho
B là trung điểm NP
C là trung điểm MP
D là trung điểm MN
Ta có AD = CB = $\frac{1}{2}$ MN
⇒ AM $\perp$ AN
Tương tự AM $\perp$ AP, AN $\perp$ AP
Gọi AM = x, AN = y, AP = z
Ta có AM² + AN² = MN²
⇔ x² + y² = 4b²
Tương tự

$AM^2+AP^2=MP^2\Rightarrow x^2+z^2=4c^2$

$AN^2+AP^2=NP^2\Rightarrow y^2+z^2=4a^2$

Ta có:

$\left\{\begin{matrix} x^2+y^2=4b^2\\ x^2+z^2=4c^2\\ y^2+z^2=4a^2 \end{matrix}\right.\Rightarrow x^2+y^2+z^2=2(a^2+b^2+c^2)$

$x^2=2(-a^2+b^2+c^2)$
$y^2=2(a^2+b^2-c^2)$
$z^2=2(a^2-b^2+c^2)$

$V_{AMNP}=\frac{1}{3}.AP.\frac{1}{2}AM.AN$

$=\frac{1}{6}AM.AN.AP=\frac{2\sqrt{2}}{6}\sqrt{(-a^2+b^2+c^2)(a^2+b^2-c^2)(a^2-b^2+c^2)}$

$=\frac{\sqrt{2}}{3}\sqrt{(-a^2+b^2+c^2)(a^2+b^2-c^2)(a^2-b^2+c^2)}$

$V_{ABCD}=\frac{1}{4}.V_{AMNP} \ (do \ dt \ BCD=\frac{1}{4} \ dt \ MNP)$

$=\frac{\sqrt{2}}{12}\sqrt{(-a^2+b^2+c^2)(a^2+b^2-c^2)(a^2-b^2+c^2)}$

Cách 2: (Sử dụng kết quả VD1)
VD 3: Cho hình hộp ABCD.A'B'C'D' có thể tích V. Tính thể tích của khối tứ diện ACB'D' theo V.
Giải

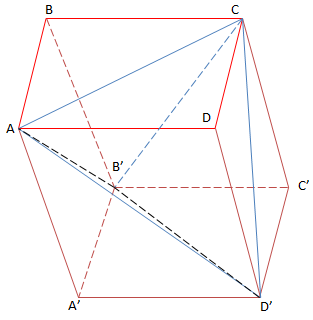
$V_{ACB'D'}=V-V_{A.A'B'D'}-V_{B'ABC}-V_{CB'D'C'}-V_{D'ACD}$
$V_{A.A'B'D'}=\frac{1}{3}.d(A,(A'B'D')).dtA'B'D'$
$=\frac{1}{3}.d(A,(A'B'D')).\frac{1}{2}.dtA'B'C'D'=\frac{1}{6}V$

Tương tự 
$V_{B'ABC}=V_{CB'D'C'}=V_{D'ACD}=\frac{V}{6}$
$V_{ACB'D'}=V-\frac{4}{6}V=\frac{1}{3}V$

Chú ý:
$V_{AA'B'D'}=\frac{1}{6}.V_{ABCD.A'B'C'D'}$

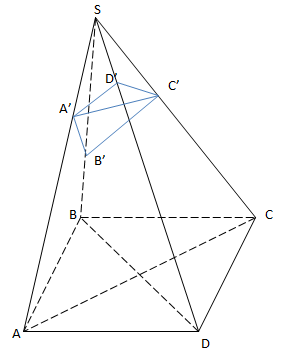
VD4: Cho hình chóp S.ABCD, có thể tích V, đáy ABCD là hình bình hành. Các điểm A', B', C' tương tư thuộc cạnh SA, SB, SC sao cho $\frac{SA'}{SA}=\frac{1}{3}, \frac{SB'}{SB}=\frac{1}{2}, \frac{SC'}{SC}=\frac{1}{5}$. Mặt phẳng (A'B'C') cắt SD tại D'.

a, Tính $\frac{SD}{SD'}$
b, Tính V_SA'B'C'D' theo V.

Giải
a,
$\frac{V_{S.A'B'C'D'}}{V_{SABCD}}=\frac{V_{SA'C'B'}}{2.V_{SACB}}+ \frac{V_{SA'C'D'}}{2.V_{SACD}}$

$=\frac{1}{2}.\frac{SA'}{SA}.\frac{SC'}{SC}.\frac{SB'}{SB}+\frac{1}{2.} \frac{SA'}{SA}.\frac{SC'}{SC}.\frac{SD'}{SD}$

Tương tự
$\frac{V_{SA'B'C'D'}}{V_{SABCD}}=\frac{1}{2}.\frac{SB'}{SB}. \frac{SD'}{SD}.\frac{SA'}{SA}+\frac{1}{2}.\frac{SB'}{SB}. \frac{SD'}{SD}.\frac{SC'}{SC} \ \ (2)$


Từ (1) (2) 

$\frac{SA'}{SA}.\frac{SC'}{SC}.\frac{SB'}{SB}+ \frac{SA'}{SA}.\frac{SC'}{SC}.\frac{SD'}{SD}= \frac{SB'}{SB}.\frac{SD'}{SD}.\frac{SA'}{SA}+ \frac{SB'}{SB}.\frac{SD'}{SD}.\frac{SC'}{SC}$

Nhân 2 vế với $\frac{SA}{SA'}.\frac{SB}{SB'}.\frac{SC}{SC'}.\frac{SD}{SD'}$

 ta có
$\frac{SD}{SD'}+\frac{SB}{SB'}=\frac{SA}{SA'}+\frac{SC}{SC'}$

$\Rightarrow \frac{SD}{SD'}=\frac{SA}{SA'}+\frac{SC}{SC'}-\frac{SB}{SB'}= 3+5-2=6$

b, Từ a)
$\frac{V_{SA'B'C'D'}}{V_{SABCD}}=\frac{1}{2}.\frac{SA'}{SA}.\frac{SC'}{SC}. \frac{SB'}{SB}+\frac{SA'}{SA}.\frac{SC'}{SC}.\frac{SD'}{SD}$

$=\frac{1}{2}.\frac{1}{3}.\frac{1}{5}.\frac{1}{2}+ \frac{1}{2}.\frac{1}{3}.\frac{1}{5}.\frac{1}{6}=\frac{1}{60}+\frac{1}{180}= \frac{1}{45}$

$\Rightarrow V_{SA'B'C'D'}= \frac{1}{45}.V$