GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
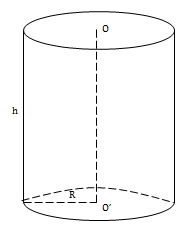
Cho hình trụ có chiều cao h, bán kính đáy là R.
\(S_{xq}=2\pi .R.h\)
\(S_{tp}=2\pi .R.h+2\pi R^2\)
II. Bài tập
Ví dụ 1: Tính diện tích xung quanh, diện tích toàn phần của hình trụ, có độh dài đường tròn đáy là 8 cm, khoảng cách giữa 2 đáy là 5 cm.
Giải
\(2R=8cm\Rightarrow R=4cm\)
Chiều cao h bằng khoảng cách giữa hai đáy bằng 5 cm
\(S_{xq}=2\pi .R.h=2\pi .4.5=40\pi (cm^2)\)
\(S_{tp}=2\pi .R.h+2\pi R^2=40\pi+2 \pi.4^2=72\pi (cm^2)\)
Ví dụ 2: Cho hình chữ nhật ABCD, có AB=3cm, AD = 4cm. Tính Sxq, Stp của hình trụ tạo thành khi cho đường gấp khúc.
a) ABCD quay quanh AB
b) BADC quay quanh BC.
Giải
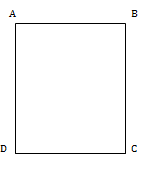
a)
Khi cho đường gấp khúc ADCB quay quanh AB ta được hình trụ có chiều cao h1 = AB = 3 (cm)
Bán kính hình tròn đáy là R1 = 4 cm
\(S_{xq}=2\pi .R_1.h_1=2\pi .4.3=24\pi (cm^2)\)
\(S_{tp}=2\pi .R_1.h_1+2\pi R_1^2=24\pi+32 \pi=56\pi (cm^2)\)
b)
Khi cho đường gấp khúc BADC quay quanh BC ta được hình trụ có chiều cao \(h_2=BC=AD=4(cm)\)
bán kính hình tròn đáy \(R_2=AB=3(cm)\)
\(S_{xq}=2\pi .R_2.h_2=2\pi .3.4=24\pi (cm^2)\)
\(S_{tp}=2\pi .R_2.h_2+2\pi R_2^2=24\pi+18 \pi=42\pi (cm^2)\)
Nhận xét: Cho hình chữ nhật ABCD có AB = k.AD.
Gọi S1, S2 l3 diện tích xung quanh của hình trụ tạo thành khi cho đường gấp khúc ADCB quay quanh AB, BADC quay quanh BC. Tính \(\frac{S_1}{S_2}\)
Giải
\(\frac{S_1}{S_2}=\frac{2\pi AD.AB+2\pi AD^2}{2\pi AB.AD+2\pi AB^2}\)
\(=\frac{2\pi .k.AD^2+2\pi AD^2}{2\pi .k.AD+2\pi.k.AD^2}=\frac{k+1}{k+k^2}=\frac{1}{k}\)
Ví dụ 3: Cho hộp hình trụ có thể tích là V. Tìm bán kính để nguyên liệu dùng làm vỏ hộp là ít nhất.
Giải
Gọi bán kính hình trụ là R, chiều cao h, ta có:
\(V=\pi .R^2.h\Rightarrow h=\frac{V}{\pi.R^2 }\)
\(S_{tp}=2\pi .R.h+2\pi R^2=2\pi R.\frac{V}{\pi R^2}+2\pi R^2\)
\(=\frac{2V}{R}+2\pi R^2=f(R)\)
\(f'(R)=-\frac{2V}{R^2}+4\pi R\)
\(f'(R)=0\Leftrightarrow 4\pi R^3=2V\)
\(\Leftrightarrow R^3=\frac{V}{2\pi }\Leftrightarrow R=\sqrt[3]{\frac{V}{2\pi }}\)
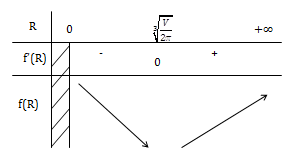
\(f(R)_{min}=f\left (\sqrt[3]{\frac{V}{2\pi }} \right )\)
\(S_{tp_{min}}\Leftrightarrow R=\left (\sqrt[3]{\frac{V}{2\pi }} \right )\)
Cách 2:
\(S_{tp}=\frac{V}{R}+\frac{V}{R}+2\pi R^2\geq 3.\sqrt[3]{\frac{V}{R}.\frac{V}{R}.2\pi R^2} =3.\sqrt[3]{2\pi .R^2}\)
\(S_{tp_{min}}=3.\sqrt[3]{2\pi .R^2}\Leftrightarrow \frac{V}{R}=2\pi .R^2 \Leftrightarrow R=\sqrt[3]{\frac{V}{2\pi }}\)














 Ra mắt HOC247 Kids nền tảng học tập Online #1
Ra mắt HOC247 Kids nền tảng học tập Online #1



